题目内容
13．
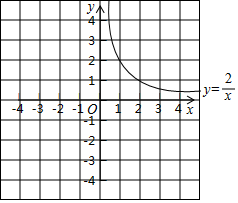函数y=$\frac{2}{x}$的图象如图所示．（1）在同一坐标系中，用描点法画下列函数的图象：
①y=$\frac{2}{x}$+1； ②y=$\frac{2}{x+1}$
列表：
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=$\frac{2}{x}$ | … | -$\frac{1}{2}$ | -$\frac{2}{3}$ | -1 | -2 | / | 2 | 1 | $\frac{2}{3}$ | $\frac{1}{2}$ | … |
| y=$\frac{2}{x}$+1 | … | $\frac{1}{2}$ | $\frac{1}{3}$ | 0 | -1 | / | 3 | 3 | $\frac{2}{3}$ | $\frac{1}{2}$ | … |
| y=$\frac{2}{x+1}$ | … | -$\frac{2}{3}$ | -1 | -2 | / | 2 | 1 | $\frac{2}{3}$ | $\frac{1}{2}$ | $\frac{2}{5}$ | … |
（2）观察图象，完成填空：
①将函数y=$\frac{2}{x}$的图象向上平移1个单位，可得函数y=$\frac{2}{x}$+1的图象；
②将函数y=$\frac{2}{x}$的图象向左平移1个单位，可得函数y=$\frac{2}{x+1}$的图象．
（3）函数y=$\frac{2}{x}$的图象经过怎样的变化，可得函数y=$\frac{x+2017}{x+2015}$的图象？（写一种即可）
分析 （1）根据题意填表和画出函数图形即可；
（2）根据图象即可得到结论；
（3）根据（2）的结论即可得到结论．
解答 解：（1）
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=$\frac{2}{x}$ | … | -$\frac{1}{2}$ | -$\frac{2}{3}$ | -1 | -2 | / | 2 | 1 | $\frac{2}{3}$ | $\frac{1}{2}$ | … |
| y=$\frac{2}{x}$+1 | … | $\frac{1}{2}$ | $\frac{1}{3}$ | 0 | -1 | / | 3 | 2 | $\frac{5}{3}$ | $\frac{3}{2}$ | … |
| y=$\frac{2}{x+1}$ | … | -$\frac{2}{3}$ | -1 | -2 | / | 2 | 1 | $\frac{2}{3}$ | $\frac{1}{2}$ | $\frac{2}{5}$ | … |
故答案为：$\frac{1}{2}，\frac{1}{3}$，0，-1，3，2，$\frac{5}{3}，\frac{3}{2}$，-$\frac{2}{3}$，-1，-2，2，1，$\frac{2}{3}，\frac{1}{2}，\frac{2}{5}$；图象如图所示；
（2）①将函数y=$\frac{2}{x}$的图象向上平移1个单位，可得函数y=$\frac{2}{x}$+1的图象；
②将函数y=$\frac{2}{x}$的图象向 左平移1个单位，可得函数y=$\frac{2}{x+1}$的图象．
故答案为：上、1； 左、1；
（3）先将函数y=$\frac{2}{x}$的图象向左平移2015个单位，得函数y$\frac{2}{x+2015}$的图象：
再将所得 图象向上平移1个单位，得函数y=$\frac{2}{x+2015}$+1，即y=$\frac{x+2017}{x+2015}$的图象．
点评 本题考查了反比例函数的图象，函数图形与几何变换，正确的作出图象是解题的关键．
练习册系列答案
综合自测系列答案
相关题目
3．下列函数中，当x＞0时y随x的增大而增大的是（ ）
| A． | y=-$\frac{2}{x}$ | B． | y=-2x | C． | y=-x-2 | D． | y=（x-2）2 |
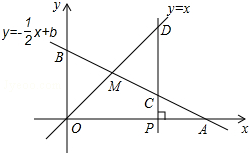如图，已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B，与函数y=x的图象交于点M，点M的横坐标为2．