题目内容
3.A(x1,y1),B(x2,y2)为平面直角坐标系内的两点,定义d(A,B)=max{|x1-x2|,|y1-y2|},并称它为A,B两点之间的“切比雪夫距离”(其中max{x,y}表示x,y中的较大值),现已知平面直角坐标系内有定点A(4,2),O为坐标原点,动点P满足d(A,P)=d(O,P),则在第一象限内动点P的轨迹的长度为2+2$\sqrt{2}$.分析 点P的轨迹如图所示(折线FEK).E(2,2),F(2,0),K(0,4),由此即可解决问题.
解答 解:由题意可知,点P的轨迹如图所示(折线FEK).E(2,2),F(2,0),K(0,4)
∴EF=2,EK=2$\sqrt{2}$
∴在第一象限内动点P的轨迹的长度为2+2$\sqrt{2}$.
故答案为2+2$\sqrt{2}$.
点评 本题考查轨迹、点的坐标等知识,解题的关键是正确寻找点P的运动轨迹,属于中考常考题型.

练习册系列答案
相关题目
13.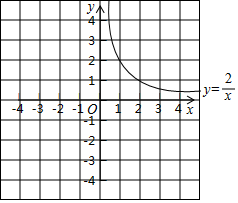 函数y=$\frac{2}{x}$的图象如图所示.
函数y=$\frac{2}{x}$的图象如图所示.
(1)在同一坐标系中,用描点法画下列函数的图象:
①y=$\frac{2}{x}$+1; ②y=$\frac{2}{x+1}$
列表:
画图象,并注明函数表达式:
(2)观察图象,完成填空:
①将函数y=$\frac{2}{x}$的图象向上平移1个单位,可得函数y=$\frac{2}{x}$+1的图象;
②将函数y=$\frac{2}{x}$的图象向左平移1个单位,可得函数y=$\frac{2}{x+1}$的图象.
(3)函数y=$\frac{2}{x}$的图象经过怎样的变化,可得函数y=$\frac{x+2017}{x+2015}$的图象?(写一种即可)
 函数y=$\frac{2}{x}$的图象如图所示.
函数y=$\frac{2}{x}$的图象如图所示.(1)在同一坐标系中,用描点法画下列函数的图象:
①y=$\frac{2}{x}$+1; ②y=$\frac{2}{x+1}$
列表:
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=$\frac{2}{x}$ | … | -$\frac{1}{2}$ | -$\frac{2}{3}$ | -1 | -2 | / | 2 | 1 | $\frac{2}{3}$ | $\frac{1}{2}$ | … |
| y=$\frac{2}{x}$+1 | … | $\frac{1}{2}$ | $\frac{1}{3}$ | 0 | -1 | / | 3 | 3 | $\frac{2}{3}$ | $\frac{1}{2}$ | … |
| y=$\frac{2}{x+1}$ | … | -$\frac{2}{3}$ | -1 | -2 | / | 2 | 1 | $\frac{2}{3}$ | $\frac{1}{2}$ | $\frac{2}{5}$ | … |
(2)观察图象,完成填空:
①将函数y=$\frac{2}{x}$的图象向上平移1个单位,可得函数y=$\frac{2}{x}$+1的图象;
②将函数y=$\frac{2}{x}$的图象向左平移1个单位,可得函数y=$\frac{2}{x+1}$的图象.
(3)函数y=$\frac{2}{x}$的图象经过怎样的变化,可得函数y=$\frac{x+2017}{x+2015}$的图象?(写一种即可)
14.如果一个三角形的两边长分别为5,12,则第三边的长可以是( )
| A. | 18 | B. | 13 | C. | 7 | D. | 5 |
11.若a<b,则下列各式一定成立的是( )
| A. | a-1<b-1 | B. | $\frac{a}{3}>\frac{b}{3}$ | C. | a2>b2 | D. | ac<bc |
 如图,直线AB、CD相交于点O,EO⊥CD,若∠AOC=35°,则∠BOE是55度.
如图,直线AB、CD相交于点O,EO⊥CD,若∠AOC=35°,则∠BOE是55度. 如图,一次函数y1=k1+b1与y2=k2+b2的图象相交于A(3,2),则不等式(k2-k1)x+b2-b1>0的解集为x<3.
如图,一次函数y1=k1+b1与y2=k2+b2的图象相交于A(3,2),则不等式(k2-k1)x+b2-b1>0的解集为x<3.