题目内容
16.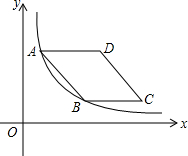 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为4$\sqrt{2}$.
如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为4$\sqrt{2}$.
分析 过点A作x轴的垂线,与CB的延长线交于点E,根据A,B两点的纵坐标分别为3,1,可得出横坐标,即可求得AE,BE,再根据勾股定理得出AB,根据菱形的面积公式:底乘高即可得出答案.
解答 解:过点A作x轴的垂线,与CB的延长线交于点E,
∵A,B两点在反比例函数y=$\frac{3}{x}$的图象上且纵坐标分别为3,1,
∴A,B横坐标分别为1,3,
∴AE=2,BE=2,
∴AB=2$\sqrt{2}$,
S菱形ABCD=底×高=2$\sqrt{2}$×2=4$\sqrt{2}$,
故答案为4$\sqrt{2}$.
点评 本题考查了菱形的性质以及反比例函数图象上点的坐标特征,熟记菱形的面积公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.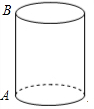 如图,有一圆柱体,底面周长为15cm,高AB=8cm,在圆柱的下底面A点处有一只蚂蚁,它想绕圆柱体侧面一周爬行到B点处,那么它们所行走得最短路程是( )
如图,有一圆柱体,底面周长为15cm,高AB=8cm,在圆柱的下底面A点处有一只蚂蚁,它想绕圆柱体侧面一周爬行到B点处,那么它们所行走得最短路程是( )
 如图,有一圆柱体,底面周长为15cm,高AB=8cm,在圆柱的下底面A点处有一只蚂蚁,它想绕圆柱体侧面一周爬行到B点处,那么它们所行走得最短路程是( )
如图,有一圆柱体,底面周长为15cm,高AB=8cm,在圆柱的下底面A点处有一只蚂蚁,它想绕圆柱体侧面一周爬行到B点处,那么它们所行走得最短路程是( )| A. | 8cm | B. | 17cm | C. | 23cm | D. | 13cm |
1. 在△ABC中,D是BC上的一点,且△ABD与△ADC的面积相等,则线段AD为△ABC的( )
在△ABC中,D是BC上的一点,且△ABD与△ADC的面积相等,则线段AD为△ABC的( )
 在△ABC中,D是BC上的一点,且△ABD与△ADC的面积相等,则线段AD为△ABC的( )
在△ABC中,D是BC上的一点,且△ABD与△ADC的面积相等,则线段AD为△ABC的( )| A. | 高 | B. | 角平分线 | C. | 中线 | D. | 不能确定 |
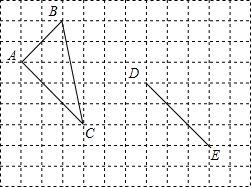 已知:如图所示的网格中有△ABC,
已知:如图所示的网格中有△ABC,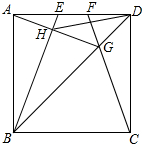 如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.
如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H. 已知:如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F,求证:四边形AFCE是菱形.
已知:如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F,求证:四边形AFCE是菱形.