题目内容
1．
在△ABC中，D是BC上的一点，且△ABD与△ADC的面积相等，则线段AD为△ABC的（ ）| A． | 高 | B． | 角平分线 | C． | 中线 | D． | 不能确定 |
分析 表示出△ABD与△ADC的面积，可推导出BD=DC，即可解答．
解答 解：作AE⊥BC，
∵△ABD与△ADC面积相等，
∴$\frac{1}{2}$BD×AE=$\frac{1}{2}$DC×AE，
∴BD=DC，
即线段AD一定是△ABC的中线．
故选C
点评 本题主要考查了三角形的面积，掌握三角形的中线分成的两个三角形的面积相等．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
11．
如果有一个正方体，它的展开图可能是下列四个展开图中的（ ）
如果有一个正方体，它的展开图可能是下列四个展开图中的（ ）| A． |  | B． |  | C． |  | D． |  |
12．
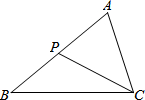如图，点P为△ABC的AB边上一点（AB＞AC），下列条件中不一定能保证△ACP∽△ABC的是（ ）
如图，点P为△ABC的AB边上一点（AB＞AC），下列条件中不一定能保证△ACP∽△ABC的是（ ）| A． | ∠ACP=∠B | B． | ∠APC=∠ACB | C． | $\frac{PC}{BC}$=$\frac{AC}{AB}$ | D． | $\frac{AC}{AB}$=$\frac{AP}{AC}$ |
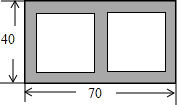如图，在长70m，宽40m的长方形花园中，欲修宽度相等的观赏路（如阴影部分所示），要使观赏路面积占总面积的$\frac{1}{8}$，则路宽x应满足的方程是（70-3x）（40-2x）=40×70×（1-$\frac{1}{8}$）．
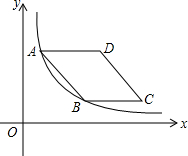如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为3，1，反比例函数y=$\frac{3}{x}$的图象经过A，B两点，则菱形ABCD的面积为4$\sqrt{2}$．
6．方程x2=2x的解是（ ）
| A． | x1=-2，x2=0 | B． | x1=$\sqrt{2}$，x2=0 | C． | x1=1，x2=2 | D． | x1=2，x2=0 |
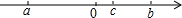有理数a、b、c在数轴上的位置如图所示，则|a-b|-|2a-c|=a+b-c．
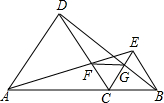已知：如图，A、C、B在同一直线上，△ADC和△BCE都是正三角形，DB、EA分别交CE、DC于G、F．求证：