题目内容
19.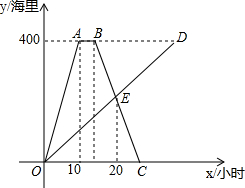 巡洋舰完成某海域巡航任务返回基地补给,同时海警船前往相同海域执怯(巡洋舰与海警船始终在同一航线上航行),巡洋舰返回基地修整5小时后立即按原路原速返回,如图是巡洋舰与海警船离各自出发地的路程y(单位:海里)与海警船航行时间x(单位:时)的承数图象.
巡洋舰完成某海域巡航任务返回基地补给,同时海警船前往相同海域执怯(巡洋舰与海警船始终在同一航线上航行),巡洋舰返回基地修整5小时后立即按原路原速返回,如图是巡洋舰与海警船离各自出发地的路程y(单位:海里)与海警船航行时间x(单位:时)的承数图象.请根据图象信息解答列问题:
(1)分别求出巡洋舰与海警船的航行速度;
(2)求出巡洋舰返回时的函数解析式,并写出自变量x的取俏范围;
(3)请直接写出巡洋舰与海警船在途中相遇的时间.
分析 (1)根据图中所给的条件即可得到结论;
(2)设出巡洋舰返回时的函数解析式分别是y=kx+b,y=kx,解方程或方程组即可得到结论;
(3)根据图象即可得到结论.
解答  解:(1)巡洋舰航行速度为:$\frac{400}{10}$=40(海里\小时),5小时走5×40=200海里,
解:(1)巡洋舰航行速度为:$\frac{400}{10}$=40(海里\小时),5小时走5×40=200海里,
∴E点的纵坐标为400-200=200,
∴E(20,200),
∴海警船的航行速度为:$\frac{200}{20}$=10(海里\小时);
(2)设出巡洋舰返回时的函数解析式分别是:y=kx+b,y=kx,把E(20,200)代入y=kx得:k=10,
∴y=10x,
把B(15,400),E(20,200)代入y=kx+b得$\left\{\begin{array}{l}{15k+b=400}\\{20k+b=200}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-40}\\{b=1000}\end{array}\right.$,
∴y=-40x+1000;
(3)由图象知:巡洋舰与海警船在途中相遇的时间为海警船出发后20小时.
点评 本题考查了行程问题的数量关系的运用,待定系数法求一次函数的解析式的运用,一次函数与一元一次方程的运用,解答时求出函数的解析式是关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
8.一次函数y=(3m-2)x+2m-1的图象交于y轴的正半轴,则m的取值范围是( )
| A. | m>$\frac{2}{3}$ | B. | m>$\frac{1}{2}$ | C. | m<$\frac{1}{2}$ | D. | m<$\frac{2}{3}$ |
9.在Rt△ABC中,∠C=90°,若AB=6,BC=2,则cosB=( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{3\sqrt{2}}{4}$ |
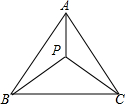 如图,等边△ABC中,AB=4,P是△ABC中的任意一点,连接PA、PB、PC,则PA+PB+PC的最小值为4$\sqrt{3}$.
如图,等边△ABC中,AB=4,P是△ABC中的任意一点,连接PA、PB、PC,则PA+PB+PC的最小值为4$\sqrt{3}$.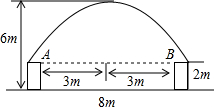 某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)
某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)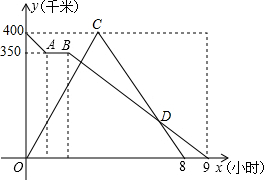 甲、乙两地相距的路程是400千米,快、慢两车同时从两地出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原路原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地,在两车行驶的过程中,两车距甲地的路程y(千米)与两车行驶时间x(小时)之间的函数图象如图所示.请结合图象解答下列间题:
甲、乙两地相距的路程是400千米,快、慢两车同时从两地出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原路原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地,在两车行驶的过程中,两车距甲地的路程y(千米)与两车行驶时间x(小时)之间的函数图象如图所示.请结合图象解答下列间题: