题目内容
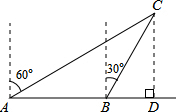 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD长多少海里?
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD长多少海里?考点:解直角三角形的应用-方向角问题
专题:
分析:根据方向角的定义及余角的性质求出∠CAD=30°,∠CBD=60°,再由三角形外角的性质得到∠CAD=30°=∠ACB,根据等角对等边得出AB=BC=20,然后解Rt△BCD,求出CD即可.
解答:解:根据题意可知∠CAD=30°,∠CBD=60°,
∵∠CBD=∠CAD+∠ACB,
∴∠CAD=30°=∠ACB,
∴AB=BC=20海里,
在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=
,
∴sin60°=
,
∴CD=12×sin60°=20×
=10
(海里).
答:海岛C到航线AB的距离CD长为10
海里.
∵∠CBD=∠CAD+∠ACB,
∴∠CAD=30°=∠ACB,
∴AB=BC=20海里,
在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=
| DC |
| BC |
∴sin60°=
| DC |
| BC |
∴CD=12×sin60°=20×
| ||
| 2 |
| 3 |
答:海岛C到航线AB的距离CD长为10
| 3 |
点评:本题考查了解直角三角形的应用,难度适中.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
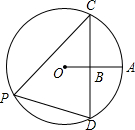 如图,点B是⊙O的半径OA的中点,且弦CD⊥OA于B,则tan∠CPD的值为( )
如图,点B是⊙O的半径OA的中点,且弦CD⊥OA于B,则tan∠CPD的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
我校一位同学从2015年元月1号开始每天记录当天的最低气温,然后绘成统计图,为了直观反应气温的变化情况,他应选择( )
| A、折线图 | B、扇形图 |
| C、条形图 | D、以上都合适 |
从3点到6点整,钟表的时针旋转的度数为( )
| A、.30° | B、60° |
| C、90° | D、120° |
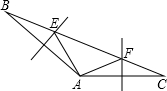 已知△ABC中,∠BAC=110°,AB、AC的垂直平分线分别交于BC于E,F,则∠EAF的度数( )
已知△ABC中,∠BAC=110°,AB、AC的垂直平分线分别交于BC于E,F,则∠EAF的度数( )| A、20° | B、40° |
| C、50° | D、60° |
 如图,△ABC中,AD是中线,AE是角平分线,CF垂直AE于点F,AB=5,AC=2,则FD的长是
如图,△ABC中,AD是中线,AE是角平分线,CF垂直AE于点F,AB=5,AC=2,则FD的长是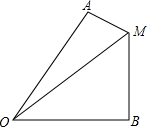 如图,已知∠AOB=60°,MA⊥OA于点A,MB⊥OB于点B,MA=2,MB=11,求OM的长.
如图,已知∠AOB=60°,MA⊥OA于点A,MB⊥OB于点B,MA=2,MB=11,求OM的长.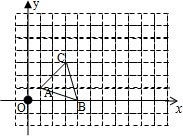 如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,请按要求完成下面的问题:
如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,请按要求完成下面的问题: 如图,?ABCD中,点E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连结AE、EF.
如图,?ABCD中,点E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连结AE、EF.