题目内容
 如图,?ABCD中,点E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连结AE、EF.
如图,?ABCD中,点E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连结AE、EF.(1)若AE平分∠BAF,求证:BE=GE;
(2)若点E是BC边上的中点,求证:∠AEF=2∠EFC.
考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)由四边形ABCD是平行四边形,DE=BC,易证得∠AEB=∠AEG,又由AE平分∠BAF,可证得△ABE≌△AGE,即可证得BE=GE;
(2)延长AE,交DC的延长线于点M,易证得△ABE≌△MCE,又由AF⊥CD,可得EF是Rt△AFM的斜边上的中线,继而证得结论.
(2)延长AE,交DC的延长线于点M,易证得△ABE≌△MCE,又由AF⊥CD,可得EF是Rt△AFM的斜边上的中线,继而证得结论.
解答:证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠DAE=∠AEB,
∵DE=BC,
∴AD=DE,
∴∠DAE=∠AED,
∴∠AEB=∠AED,
∵AE平分∠BAF,
∴∠BAE=∠GAE,
在△ABE和△AGE中,
,
∴△ABE≌△AGE(ASA),
∴BE=GE;
(2)延长AE,交DC的延长线于点M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAF=∠AFD,∠M=∠BAE,
∵点E是BC边上的中点,
∴BE=CE,
在△ABE和△MCE中,
,
∴△ABE≌△MCE(AAS),
∴AE=ME,
∵AF⊥CD,
∴EF=AE=EM=
AM,
∴∠M=∠EFC,
∴∠AEF=∠BAE+∠EFC=2∠EFC.
∴AD∥BC,AD=BC,
∴∠DAE=∠AEB,
∵DE=BC,
∴AD=DE,
∴∠DAE=∠AED,
∴∠AEB=∠AED,
∵AE平分∠BAF,
∴∠BAE=∠GAE,
在△ABE和△AGE中,
|
∴△ABE≌△AGE(ASA),
∴BE=GE;

(2)延长AE,交DC的延长线于点M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAF=∠AFD,∠M=∠BAE,
∵点E是BC边上的中点,
∴BE=CE,
在△ABE和△MCE中,
|
∴△ABE≌△MCE(AAS),
∴AE=ME,
∵AF⊥CD,
∴EF=AE=EM=
| 1 |
| 2 |
∴∠M=∠EFC,
∴∠AEF=∠BAE+∠EFC=2∠EFC.
点评:此题考查了平行四边形的性质、等腰三角形的性质、直角三角形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
若a>b,则下列不等式中一定成立的是( )
A、
| ||
B、
| ||
| C、-a>-b | ||
| D、a-b>0 |
已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则k的值为( )
| A、3 | B、-3 |
| C、3或-3 | D、k的值不确定 |
已知△ABC≌△DEF,且△ABC的周长为15,若AC=4,EF=6,则AB=( )
| A、4 | B、5 | C、6 | D、5或6 |
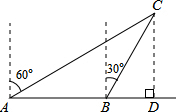 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD长多少海里?
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD长多少海里?