题目内容
14.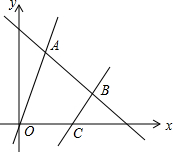 如图,直线l是一次函数y=-x+8的图象,点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,正比例函数y=kx的图象经过点A,一次函数y=2x+b的图象经过点B,且与x轴相交于点C.
如图,直线l是一次函数y=-x+8的图象,点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,正比例函数y=kx的图象经过点A,一次函数y=2x+b的图象经过点B,且与x轴相交于点C.(1)求k的值;
(2)求点C的坐标;
(3)求四边形OABC的面积.
分析 (1)根据题意得到点A坐标为(2,6),点B坐标为(5,3),代入y=kx即可得到结论;
(2)由于一次函数y=2x+b的图象经过点B,得到3=2×5+b,于是得到结论;
(3)设直线x轴相交于点D,得到点D坐标为(8,0),根据图形的面积公式即可得到结论.
解答 解:(1)∵点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,
∴点A的纵坐标为6,点B的横坐标为5,
即点A坐标为(2,6),点B坐标为(5,3),
∵正比例函数y=kx的图象经过点A,
∴2k=6,
∴k=3;
(2)∵一次函数y=2x+b的图象经过点B,
∴3=2×5+b,∴b=-7,
∴一次函数的解析式为y=2x-7,
∵一次函数y=2x-7的图象与x轴相交于点C,
∴点C坐标为($\frac{7}{2}$,0);
(3)设直线x轴相交于点D,则点D坐标为(8,0),
可得OC=$\frac{7}{2}$,OD=8,CD=$\frac{9}{2}$,
∵点A到x轴的距离为6,点B到x轴的距离为3,
∴S四边形OABC=S△OAD-S△CBD=$\frac{1}{2}×$8×6-$\frac{1}{2}×\frac{9}{2}$×3=$\frac{69}{4}$.
点评 本题考查了一次函数图象上点的坐标特征,求一次函数的解析式,三角形的面积,正确的理解题意是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 石墨烯(Graphene)是一种由碳原子以sp2杂化轨道组成的六角型呈蜂巢晶格的平面薄膜,是目前发现的厚度最薄、强度最大、导电导热性能最强的一种新型纳米材料,其厚度仅为0.334纳米.数据0.334纳米用科学记数法可以表示为( )
石墨烯(Graphene)是一种由碳原子以sp2杂化轨道组成的六角型呈蜂巢晶格的平面薄膜,是目前发现的厚度最薄、强度最大、导电导热性能最强的一种新型纳米材料,其厚度仅为0.334纳米.数据0.334纳米用科学记数法可以表示为( )
 石墨烯(Graphene)是一种由碳原子以sp2杂化轨道组成的六角型呈蜂巢晶格的平面薄膜,是目前发现的厚度最薄、强度最大、导电导热性能最强的一种新型纳米材料,其厚度仅为0.334纳米.数据0.334纳米用科学记数法可以表示为( )
石墨烯(Graphene)是一种由碳原子以sp2杂化轨道组成的六角型呈蜂巢晶格的平面薄膜,是目前发现的厚度最薄、强度最大、导电导热性能最强的一种新型纳米材料,其厚度仅为0.334纳米.数据0.334纳米用科学记数法可以表示为( )| A. | 0.334×10-9米 | B. | 3.34×10-9米 | C. | 3.34×10-10米 | D. | 3.34×10-8米 |
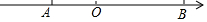 如图,在数轴上有A、B两点,A、B两点所表示的有理数分别是2k-4和-2k+6,且k为最大的负整数.
如图,在数轴上有A、B两点,A、B两点所表示的有理数分别是2k-4和-2k+6,且k为最大的负整数.
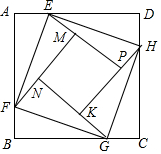 如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )