题目内容
5.已知点P时第二、四象限角平分线上的一点,若点P在第二象限且点P到原点的距离为4,那么点P的坐标为(2$\sqrt{2}$,2$\sqrt{2}$).分析 根据第二象限内点的横坐标是负数,纵坐标是正数,角平分线上的点到角的两边距离相等设点P的坐标为(-a,a)(a>0),然后利用勾股定理列式求解即可.
解答 解:∵点P是第二、四象限角平分线上的一点,且点P在第二象限,
∴设点P的坐标为(-a,a),(a>0),
∵点P到原点的距离为4,
∴(-a)2+a2=42,
解得a=2$\sqrt{2}$,
所以,点P的坐标为(2$\sqrt{2}$,2$\sqrt{2}$).
故答案为:(2$\sqrt{2}$,2$\sqrt{2}$).
点评 本题考查了点的坐标,主要利用了第二象限内点的横坐标是负数,纵坐标是正数和角平分线上的点到角的两边距离相等.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
17.下列说法中错误的是( )
| A. | 如果整数a是整数b的倍数,那么b是a的因数 | |
| B. | 一个合数至少有3个因数 | |
| C. | 在正整数中,除2外所有的偶数都是合数 | |
| D. | 在正整数中,除了素数都是合数 |
15.4的绝对值可表示为( )
| A. | -4 | B. | |4| | C. | $\sqrt{4}$ | D. | $\frac{1}{4}$ |
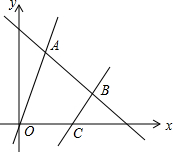 如图,直线l是一次函数y=-x+8的图象,点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,正比例函数y=kx的图象经过点A,一次函数y=2x+b的图象经过点B,且与x轴相交于点C.
如图,直线l是一次函数y=-x+8的图象,点A、B在直线l上,点A的横坐标为2,点B的纵坐标为3,正比例函数y=kx的图象经过点A,一次函数y=2x+b的图象经过点B,且与x轴相交于点C.