题目内容
9. 某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘,商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘,商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 60 | 122 | 240 | 298 | 476 | 604 |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | 0.6 | 0.59 | 0.604 |
(2)请估计当n很大时,频率将会接近0.6.假如你去转动转盘一次,你获得“洗衣粉”的概率估计值是0.6.(结果精确到0.1)
分析 (1)根据频率的定义计算n=298时的频率和频率为0.59时的频数;
(2)从表中频率的变化,可得到估计当n很大时,频率将会接近0.6,然后根据利用频率估计概率得“可乐”的概率约是0.6;
解答 解:(1):
| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 60 | 122 | 240 | 298 | 472 | 604 |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | 0.6 | 0.59 | 0.604 |
故答案为:0.6,472;0.6,0.6.
点评 本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
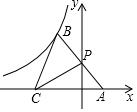 如图,双曲线y=$\frac{k}{x}$经过第二象限的点B,点P在y轴上,点A在x轴上,且点B与点A关于点P对称,若OC=2OA,△BCP的面积为4,则k的值是-$\frac{16}{3}$.
如图,双曲线y=$\frac{k}{x}$经过第二象限的点B,点P在y轴上,点A在x轴上,且点B与点A关于点P对称,若OC=2OA,△BCP的面积为4,则k的值是-$\frac{16}{3}$.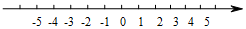 在数轴上表示下列各数,并用“<”连接起来.
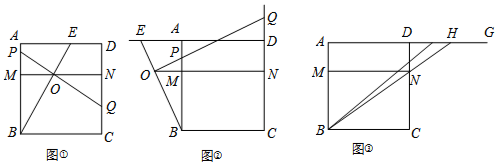
在数轴上表示下列各数,并用“<”连接起来.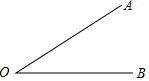 已知:∠AOB,如图,利用尺规作∠CDE,使∠CDE=∠AOB.
已知:∠AOB,如图,利用尺规作∠CDE,使∠CDE=∠AOB.