题目内容
20.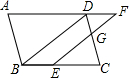 如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )
如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )| A. | $\frac{25a}{8}$ | B. | $\frac{25a}{9}$ | C. | $\frac{25a}{16}$ | D. | $\frac{16a}{9}$ |
分析 根据平行四边形的性质得到AD=BC,AD∥BC,推出四边形BEFD是平行四边形,得到BE=DF,根据相似三角形的性质得到S△CEG=$\frac{9}{16}$a,于是得到结论.
解答 解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵EF∥BD,
∴四边形BEFD是平行四边形,
∴BE=DF,
∵$\frac{DF}{AD}$=$\frac{2}{5}$,
∴$\frac{DF}{CE}$=$\frac{2}{3}$,$\frac{CE}{BC}$=$\frac{3}{5}$,
∵EG∥BD,
∴△CGE∽△CBD,
∴$\frac{{S}_{△CEG}}{{S}_{△CBD}}$=($\frac{CE}{CB}$)2=$\frac{9}{25}$,
∴$\frac{{S}_{△CEG}}{S四边形BDGE}$=$\frac{9}{16}$,
∵S四边形BDGE=a,
∴S△CEG=$\frac{9}{16}$a,
∴S△BCD=$\frac{9}{16}$a+a=$\frac{25}{16}$a,
∴S平行四边形ABCD=2S△BCD=$\frac{25}{8}$a,
故选A.
点评 本题考查了相似三角形的判定和性质,平行四边形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
9.下列整式中,属于多项式的是( )
| A. | a-2b | B. | -2ab | C. | -2 | D. | a |
8.下列说法不正确的是( )
| A. | $\frac{1}{25}$的平方根是±$\frac{1}{5}$ | B. | -9是81的一个平方根 | ||
| C. | 0.2的算术平方根是0.01 | D. | -27的立方根是-3 |
 ,则x的值为( )
,则x的值为( ) B.
B.  C.
C.  D.
D. 
 菱形ABCD的边AB为5,对角线AC为8,则菱形ABCD的面积为24.
菱形ABCD的边AB为5,对角线AC为8,则菱形ABCD的面积为24.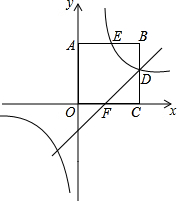 已知,正方形OABC在平面直角坐标系中的位置如图所示,点A的坐标为(0,3),双曲线y1=$\frac{k}{x}$分别交AB,BC于点E,D,直线y2=x-1过点D与x轴正半轴交于点F.
已知,正方形OABC在平面直角坐标系中的位置如图所示,点A的坐标为(0,3),双曲线y1=$\frac{k}{x}$分别交AB,BC于点E,D,直线y2=x-1过点D与x轴正半轴交于点F.