题目内容
17. 如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=$\sqrt{3}$cm,将△ABC绕点B旋转到△A'BC'的位置,且使A,B,C'三点在同一条直线上,则点C经过的最短路线的长度是多少?
如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=$\sqrt{3}$cm,将△ABC绕点B旋转到△A'BC'的位置,且使A,B,C'三点在同一条直线上,则点C经过的最短路线的长度是多少?
分析 点C经过的最短路线的长度即以BC为半径,以B为圆心的圆中,圆心角∠CBC′所对应的弧长.
解答 解:∵在Rt△ABC中,∠C=90°,∠A=60°,BC=$\sqrt{3}$cm,
∴∠ABC=30°,BC=$\sqrt{3}$cm,∠CBC′=150°,
根据弧长公式L=$\frac{nπr}{180}=\frac{150×π×\sqrt{3}}{180}=\frac{5\sqrt{3}}{6}π$.
点评 此题考查轨迹问题,关键是根据旋转的性质,求出∠CRC′的度数,利用弧长公式求出即可.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
2.在-1、+7、0、-$\frac{2}{5}$、3.14中,正数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.大刚和小亮在五次百米跑训练中,所测成绩如图所示,根据图中的信息,回答下列问题: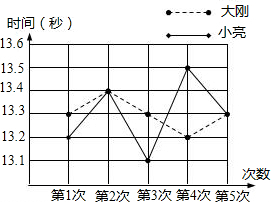
(1)两人每次的成绩(单位:s)
(2)分别计算他们的平均数和方差,并对折线的走势进行简要分析,你认为他们二人中谁的成绩好一些?

(1)两人每次的成绩(单位:s)
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 大刚 | 13.3 | 13.4 | 13.3 | 13.2 | 13.3 |
| 小亮 | 13.2 | 13.4 | 13.1 | 13.5 | 13.3 |