题目内容
7.抛物线y=ax2+bx+c经过点(4,-5)且对称轴是直线x=2,则代数式4a+b-c的值为-5.分析 把已知点的坐标代入结合对称轴公式可得到关于a、b、c的关系式,可求得答案.
解答 解:
∵y=ax2+bx+c经过点(4,-5),
∴16a+4b+c=-5,
∵对称轴是直线x=2,
∴-$\frac{b}{2a}$=2,
∴b=-4a,
∴16a-16a+c=-5,解得c=-5,
∴4a+b+c=4a-4a+c=-5,
故答案为:-5.
点评 本题主要考查二次函数的性质,掌握函数图象上点的坐标满足函数解析式是解题的关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
15.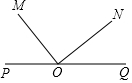 如图所示,在一条直线上顺次有P、O、Q三点,自O点在这条直线的同侧引两条射线OM、ON,如果∠MON=90°(∠POM为锐角),那么∠POM的余角是( )
如图所示,在一条直线上顺次有P、O、Q三点,自O点在这条直线的同侧引两条射线OM、ON,如果∠MON=90°(∠POM为锐角),那么∠POM的余角是( )
 如图所示,在一条直线上顺次有P、O、Q三点,自O点在这条直线的同侧引两条射线OM、ON,如果∠MON=90°(∠POM为锐角),那么∠POM的余角是( )
如图所示,在一条直线上顺次有P、O、Q三点,自O点在这条直线的同侧引两条射线OM、ON,如果∠MON=90°(∠POM为锐角),那么∠POM的余角是( )| A. | ∠MOQ | B. | ∠MON | C. | ∠NOQ | D. | ∠PON |
 如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=$\sqrt{3}$cm,将△ABC绕点B旋转到△A'BC'的位置,且使A,B,C'三点在同一条直线上,则点C经过的最短路线的长度是多少?
如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=$\sqrt{3}$cm,将△ABC绕点B旋转到△A'BC'的位置,且使A,B,C'三点在同一条直线上,则点C经过的最短路线的长度是多少?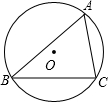 如图,△ABC内接于⊙O,已知AB=c,BC=a,AC=b,⊙O的半径为R.
如图,△ABC内接于⊙O,已知AB=c,BC=a,AC=b,⊙O的半径为R. 如图的数字三角形有一定的规律,请按规律填上空缺的数.
如图的数字三角形有一定的规律,请按规律填上空缺的数.