题目内容
11.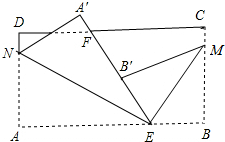 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数.并直接写出∠B′ME互余的角.
如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,求∠NEM的度数.并直接写出∠B′ME互余的角.
分析 先由翻折的性质得到∠AEN=∠A′EN,∠BEM=∠B′EM,从而可知∠NEM=$\frac{1}{2}$×180°=90°,然后根据余角的定义找出∠B′ME的余角即可.
解答 解:由翻折的性质可知:∠AEN=∠A′EN,∠BEM=∠B′EM.
∠NEM=∠A′EN+∠B′EM=$\frac{1}{2}∠AEA′+\frac{1}{2}∠B′EB$=$\frac{1}{2}$×180°=90°.
由翻折的性质可知:∠MB′E=∠B=90°.
由直角三角形两锐角互余可知:∠B′ME的一个余角是∠B′EM.
∵∠BEM=∠B′EM,
∴∠BEM也是∠B′ME的一个余角.
∵∠NBF+∠B′EM=90°,
∴∠NEF=∠B′ME.
∴∠ANE、∠A′NE是∠B′ME的余角.
综上所述,∠B′ME的余角有∠ANE、∠A′NE、∠B′EM、∠BEM.
点评 本题主要考查的是翻折的性质、余角的定义,掌握翻折的性质是解题的关键.

练习册系列答案
相关题目
19.用带符号键 的计算器,按键如下
的计算器,按键如下 ,则该输出结果为( )
,则该输出结果为( )
 的计算器,按键如下
的计算器,按键如下 ,则该输出结果为( )
,则该输出结果为( )| A. | 17 | B. | 81 | C. | -64 | D. | 64 |
6. 如图,数轴上的点A和点B分别表示数a与数b,下列结论中正确的是( )
如图,数轴上的点A和点B分别表示数a与数b,下列结论中正确的是( )
 如图,数轴上的点A和点B分别表示数a与数b,下列结论中正确的是( )
如图,数轴上的点A和点B分别表示数a与数b,下列结论中正确的是( )| A. | a>b | B. | |a|<|b| | C. | a<-b | D. | a+b<0 |
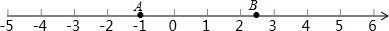
 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFC=115°,则∠AED′的度数为50度.
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFC=115°,则∠AED′的度数为50度.