题目内容
5．以下列各组数为边长，能组成直角三角形的是（ ）| A． | 2，3，4 | B． | 10，8，6 | C． | 8，25，24 | D． | 7，15，12 |
分析 根据勾股定理的逆定理可知，当三角形中三边的关系为：a2+b2=c2时，该三角形为直角三角形．
解答 解：A、22+32≠42，不符合勾股定理的逆定理，不能组成直角三角形，故错误；
B、62+82=102，符合勾股定理的逆定理，能组成直角三角形，故正确；
C、82+242≠252，不符合勾股定理的逆定理，不能组成直角三角形，故错误；
D、72+122≠152，不符合勾股定理的逆定理，不能组成直角三角形，故错误．
故选B．
点评 此题考查了勾股定理的逆定理：已知三角形ABC的三边满足：a2+b2=c2时，则三角形ABC是直角三角形．解答时，只需看两较小数的平方和是否等于最大数的平方．
练习册系列答案
金钥匙试卷系列答案
相关题目
15．
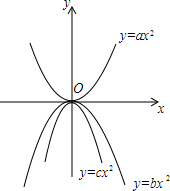抛物线y=ax2、y=bx2、y=cx2的图象如图所示，则a、b、c的大小关系是（ ）
抛物线y=ax2、y=bx2、y=cx2的图象如图所示，则a、b、c的大小关系是（ ）| A． | a＞b＞c | B． | a＞c＞b | C． | c＞a＞b | D． | c＞b＞a |
在△ABC中，∠A=50°，OB，OC分别平分∠ABC和∠ACB，则∠BOC=115度．
14．
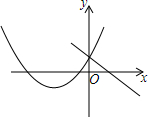已知二次函数y=ax2+bx+c的图象如图所示，则下列结论正确的是（ ）
已知二次函数y=ax2+bx+c的图象如图所示，则下列结论正确的是（ ）| A． | ab＞0，c＞0 | B． | ab＞0，c＜0 | C． | ab＜0，c＞0 | D． | ab＜0，c＜0 |
15．
如图，AB、CD相交于O点，AO=BO，CO=DO，则图中全等三角形共有（ ）
如图，AB、CD相交于O点，AO=BO，CO=DO，则图中全等三角形共有（ ）| A． | 2对 | B． | 3对 | C． | 4对 | D． | 5对 |