��Ŀ����
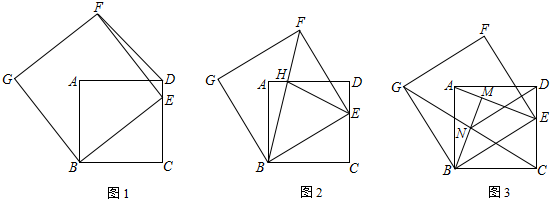
9����ͼ������ABOD������OB��OD������������������ϣ�OD=3���������뷴����������ͼ��ֱ��ཻ�ڵ�E��F����DE=2������E��EH��x���ڵ�H������F��FG��EH�ڵ�G������������⣺��1���÷����������Ľ���ʽ��ʲô��
��2�����ı���AEGFΪ������ʱ����F�������Ƕ��٣�
��3���ڣ�2���������£�����ƽ�����Ƿ���ڵ�C��ʹ�õ�C��D��H��F����ƽ���ı��Σ������ڣ���ֱ��д����C�����ꣻ�������ڣ���˵�����ɣ�
��4���ڣ�2���������£���һ��̽������P���߶�AD������һ�㣬����HP���ڵ�һ��������PQ��HP����PQ=HP������P�ӵ�D�˶���A�Ĺ����У���ֱ��д����Q������·������

���� ��1���跴������������ʽΪy=$\frac{k}{x}$���ѵ�E������뼴�ɽ�����⣮
��2���������α߳�Ϊa�����F���꣨2+a��3-a�������뷴������������ʽ�����ɽ�����⣮
��3�����ڣ����������ĵ�C��������
��4����Q�˶��Ĺ켣���߶�Q��Q�壬��Rt��Q��FQ���У�����Q��Q��=$\sqrt{2}$FQ�䣬���ɽ�����⣮
��� �⣺��1���跴������������ʽΪy=$\frac{k}{x}$��
�������E���꣨2��3��������y=$\frac{k}{x}$���õ�k=6��
�෴������������ʽΪy=$\frac{6}{x}$��
��2���������α߳�Ϊa�����F���꣨2+a��3-a����
��F��2+a��3-a������y=$\frac{6}{x}$�ã�2+a����3-a��=6��
���a=1��0����������
���F���꣨3��2����
��3�����ڣ�����ͼ�У�����C���꣨1��5����-1��1����5��-1��ʱ����C��D��H��F����ƽ���ı��Σ�
��4����ͼ��
�ٵ���P��D�غ�ʱ���ɡ�DHO�ա�DQ��A����֪��DAQ��=��DOH=90�㣬
��ʱB��A��Q�乲�ߣ�AQ��=OH=2��
�ڵ���P���߶�AD��ʱ����QM��DA��M����QN��BA��N���ɡ�PHE�ա�QPM��֪PM=HE=AD��QM=PE��
��PD=AM=NQ��
��AQ��=OH=DE��AN=MQ=PE��
��NQ��=DP=AM=NQ��
���NQQ���ǵ��������Σ�
���QQ��B=45�㣬
�۵���P��A�غ�ʱ���ɡ�AHE�ա�AQ��F��֪��AEH=��Q��FA=90�㣬
������������Q�˶��Ĺ켣���߶�Q��Q�壬
��Rt��Q��FQ����Q��Q��=$\sqrt{2}$FQ��=3$\sqrt{2}$��
���� ���⿼�鷴���������ۺ��⡢ƽ���ı��ε��ж������ʡ�ȫ�������ε��ж������ʡ��켣��֪ʶ������Ĺؼ������Ӧ�ô���ϵ����ȷ����������ʽ��ѧ��������ʼ����յ�Ѱ�ҹ켣�������п�ѹ���⣮

 ��ͼ����֪AB��FG��AC��EH��BG=HC����֤��$\frac{AF}{AC}$=$\frac{AE}{AB}$��
��ͼ����֪AB��FG��AC��EH��BG=HC����֤��$\frac{AF}{AC}$=$\frac{AE}{AB}$��