题目内容
13.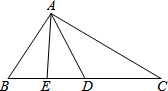 已知,如图,AD是△ABC的中线,AE是△ABD的中线,AB=DC,∠BAD=∠BDA,求证:AC=2AE.
已知,如图,AD是△ABC的中线,AE是△ABD的中线,AB=DC,∠BAD=∠BDA,求证:AC=2AE.
分析 取AB的中点F,连接DF.证明DF是△ABC的中位线,由三角形中位线定理得出DF∥AC且DF=$\frac{1}{2}$AC,由SAS可证△ADF≌△ADE,再根据全等三角形的性质即可得出结论.
解答 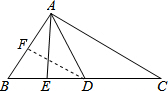 证明:取AB的中点F,连接DF.如图所示:
证明:取AB的中点F,连接DF.如图所示:
∵∠ADB=∠BAD,
∴BD=AB,
又∵CD=AB,
∴CD=BD,即D为BC中点,
∵F是AB中点,
∴DF是△ABC的中位线,
∴DF∥AC且DF=$\frac{1}{2}$AC,
又∵AB=BD,E、F分别为BD、AB中线,
∴DE=AF=$\frac{1}{2}$AB=$\frac{1}{2}$BD,
∵∠ADB=∠BAD,
∴∠FAD=∠EDA,
在△ADF与△DAE中,$\left\{\begin{array}{l}{AD=DA}&{\;}\\{∠FAD=∠EDA}&{\;}\\{DE=AF}&{\;}\end{array}\right.$
∴△ADF≌△DAE(SAS),
∴DF=AE,
∴AC=2DF=2AE.
点评 考查了等腰三角形的性质,全等三角形的判定和性质,三角形中位线定理;通过作辅助线构造三角形全等是解决问题的关键解题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
2.若点B在直线AC上,AB=10,BC=5,则A、C两点间的距离是( )
| A. | 5 | B. | 15 | C. | 5或15 | D. | 不能确定 |
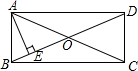 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作BD的垂线,垂足为E,若∠EAD=3∠BAE,则∠AOE=45°.
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作BD的垂线,垂足为E,若∠EAD=3∠BAE,则∠AOE=45°.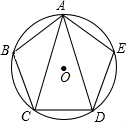 如图,正五边形ABCD内接于⊙O,连接对角线AC,AD,则下列结论:①BC∥AD;②∠BAE=3∠CAD;③△BAC≌△EAD;④AC=2CD.其中判断正确的是①②③.(填序号)
如图,正五边形ABCD内接于⊙O,连接对角线AC,AD,则下列结论:①BC∥AD;②∠BAE=3∠CAD;③△BAC≌△EAD;④AC=2CD.其中判断正确的是①②③.(填序号) 如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为8.
如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为8.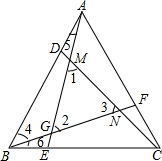 如图,△ABC为等边角形,点D,E,F分别为AB,BC,CA上的一点,且AD=BE=CF,AE,BF,CD分别相交于点G,N,M,试判断△MNG的形状并证明.
如图,△ABC为等边角形,点D,E,F分别为AB,BC,CA上的一点,且AD=BE=CF,AE,BF,CD分别相交于点G,N,M,试判断△MNG的形状并证明. 如图,已知点D在AE上,BD=CD,∠BDE=∠CDE.求证:AE是∠BAC的平分线.
如图,已知点D在AE上,BD=CD,∠BDE=∠CDE.求证:AE是∠BAC的平分线.