题目内容
5. 如图,已知点D在AE上,BD=CD,∠BDE=∠CDE.求证:AE是∠BAC的平分线.
如图,已知点D在AE上,BD=CD,∠BDE=∠CDE.求证:AE是∠BAC的平分线.
分析 由“SAS”判定△ABD≌△ACD,得出对应角相等∠BAD=∠CAD即可.
解答 证明:∵∠BDE=∠CDE.
∴∠ADB=∠ADC,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{BD=CD}&{\;}\\{∠ADB=∠ADC}&{\;}\\{AD=AD}&{\;}\end{array}\right.$,
∴△ABD≌△ACD(SAS),
∴∠BAD=∠CAD,
∴AE是∠BAC的平分线.
点评 本题考查了全等三角形的判定与性质;证明△ABD≌△ACD是解决问题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
15.下列命题中假命题的是( )
| A. | 同位角相等 | |
| B. | 同旁内角互补,两直线平行 | |
| C. | 等角的余角相等 | |
| D. | 过一点能且只能作一条直线和直线平行 |
 如图,在等边三角形ABC中AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,若BE=2,则AF=6.
如图,在等边三角形ABC中AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,若BE=2,则AF=6.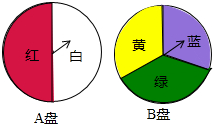 小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么配成了紫色.
小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么配成了紫色.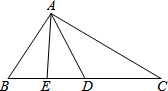 已知,如图,AD是△ABC的中线,AE是△ABD的中线,AB=DC,∠BAD=∠BDA,求证:AC=2AE.
已知,如图,AD是△ABC的中线,AE是△ABD的中线,AB=DC,∠BAD=∠BDA,求证:AC=2AE.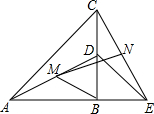 如图,点B为AE上一点,点D在BC上,AB=BC,BD=BE,∠ABC=90°,M、N分别是AD、CE的中点,求∠BMN的度数.
如图,点B为AE上一点,点D在BC上,AB=BC,BD=BE,∠ABC=90°,M、N分别是AD、CE的中点,求∠BMN的度数.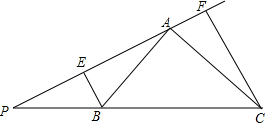 如图,在Rt△ABC中,∠BAC=90°,AB=AC,P为CB延长线上一点,过B、C两点分别作直线AP的垂线BE、CF,E、F分别为垂足,且满足∠FPC=30°,求证:$\frac{1}{2}$BC=EF-PB.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,P为CB延长线上一点,过B、C两点分别作直线AP的垂线BE、CF,E、F分别为垂足,且满足∠FPC=30°,求证:$\frac{1}{2}$BC=EF-PB. 如图,A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接CD、AE交于点P,并分别交BE、BD于N、M,连按MN,下列结论中:①AE=CD;②AM=DP;③MN∥AC;④若AB=2BC,连接DE,则DE⊥BE;⑤BP平分∠APC;⑥将△BCE绕B点任意旋转到一个角度时,DN=AM总成立.正确的结论有①③④⑤(填写出所有正确的序号)
如图,A、B、C在一条直线上,△ABD、△BCE均为等边三角形,连接CD、AE交于点P,并分别交BE、BD于N、M,连按MN,下列结论中:①AE=CD;②AM=DP;③MN∥AC;④若AB=2BC,连接DE,则DE⊥BE;⑤BP平分∠APC;⑥将△BCE绕B点任意旋转到一个角度时,DN=AM总成立.正确的结论有①③④⑤(填写出所有正确的序号)