题目内容
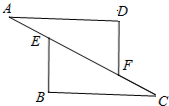如图，在△ADF与△CBE中，点A、E、F、C在同一直线上，已知AD∥BC，AD=CB，AE=CF．求证：DF=BE．考点：全等三角形的判定与性质
专题：证明题
分析：易证∠A=∠C和AF=CE，即可证明△ADF≌△CBE，根据全等三角形对应边相等的性质即可解题．
解答：证明：∵AD∥BC，
∴∠A=∠C，
∵AE=CF，
∴AE+EF=CF+EF，即AF=CE，
在△ADF和△CBE中，
，
∴△ADF≌△CBE（SAS），
∴DF=BE．
∴∠A=∠C，
∵AE=CF，
∴AE+EF=CF+EF，即AF=CE，
在△ADF和△CBE中，
|
∴△ADF≌△CBE（SAS），
∴DF=BE．
点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△ADF≌△CBE是解题的关键．
练习册系列答案
相关题目
已知a-b=1，b-c=2，那么代数式（a-c）2-2（c-a）+1的值为（ ）
| A、12 | B、14 | C、16 | D、18 |
如图，已知点E、F分别是△ABC中AC、AB边的中点，BE与CF相交于点G，FG=2，则CG的长为
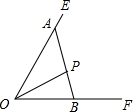如图，∠EOF内有一定点P，过点P的一条直线分别交射线OE于A，射线OF于B．当满足下列哪个条件时，△AOB的面积一定最小（ ）| A、OA=OB |
| B、OP为△AOB的角平分线 |
| C、OP为△AOB的高 |
| D、OP为△AOB的中线 |
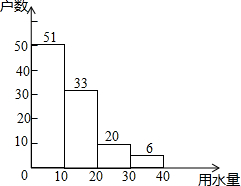某小区300户家庭，从中随机抽取了100户，调查了他们5月份的用水量情况，结果如图所示．