题目内容
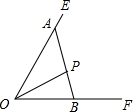 如图,∠EOF内有一定点P,过点P的一条直线分别交射线OE于A,射线OF于B.当满足下列哪个条件时,△AOB的面积一定最小( )
如图,∠EOF内有一定点P,过点P的一条直线分别交射线OE于A,射线OF于B.当满足下列哪个条件时,△AOB的面积一定最小( )| A、OA=OB |
| B、OP为△AOB的角平分线 |
| C、OP为△AOB的高 |
| D、OP为△AOB的中线 |
考点:三角形的面积
专题:
分析:当点P是AB的中点时S△AOB最小;过点P的另一条直线CD交OE、OF于点C、D,设PD<PC,过点A作AG∥OF交CD于G,由全等三角形的性质可以得出S四边形AODG=S△AOB,S四边形AODG<S△COD,从而求得S△AOB<S△COD,即可得出结论;
解答:解:当点P是AB的中点时S△AOB最小;
如图, 过点P的另一条直线CD交OE、OF于点C、D,设PD<PC,过点A作AG∥OF交CD于G,
过点P的另一条直线CD交OE、OF于点C、D,设PD<PC,过点A作AG∥OF交CD于G,
在△APG和△BPD中,
,
∴△APG≌△BPD(ASA),
S四边形AODG=S△AOB.
∵S四边形AODG<S△COD,
∴S△AOB<S△COD,
∴当点P是AB的中点时S△AOB最小;
故选:D.
如图,
 过点P的另一条直线CD交OE、OF于点C、D,设PD<PC,过点A作AG∥OF交CD于G,
过点P的另一条直线CD交OE、OF于点C、D,设PD<PC,过点A作AG∥OF交CD于G,在△APG和△BPD中,
|
∴△APG≌△BPD(ASA),
S四边形AODG=S△AOB.
∵S四边形AODG<S△COD,
∴S△AOB<S△COD,
∴当点P是AB的中点时S△AOB最小;
故选:D.
点评:本题考查了全等三角形的判定及性质的运用,四边形的面积和三角形的面积的关系,解答时建立数学模型解答是关键.

练习册系列答案
相关题目
下列方程中是一元一次方程的有( )
| A、x+3=y+2 | ||
| B、1-3(1-2x)=-2(5-3x) | ||
C、x-1=
| ||
D、
|
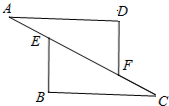 如图,在△ADF与△CBE中,点A、E、F、C在同一直线上,已知AD∥BC,AD=CB,AE=CF.求证:DF=BE.
如图,在△ADF与△CBE中,点A、E、F、C在同一直线上,已知AD∥BC,AD=CB,AE=CF.求证:DF=BE. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,若关于x的一元二次方程ax2+bx+c+m=0有实数根,则m的取值范围是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,若关于x的一元二次方程ax2+bx+c+m=0有实数根,则m的取值范围是