题目内容
1.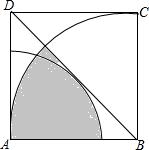 如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )
如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )| A. | π-2 | B. | $\frac{π}{2}-1$ | C. | $\frac{5π}{4}-1$ | D. | $\frac{3π}{4}-1$ |
分析 连接AC交BD于O,由正方形的性质得出OA=OB=$\frac{1}{2}$BD,AC⊥BD,∠BAD=90°,AB=AD=2,∠BAO=∠ABF=45°,由勾股定理求出BD,得出OA=OB=$\sqrt{2}$,求出△AOB的面积、扇形AOE的面积、扇形ABF的面积,即可得出图中阴影部分的面积.
解答 解:连接AC交BD于O,如图所示:
∵四边形ABCD是正方形,
∴OA=OB=$\frac{1}{2}$BD,AC⊥BD,∠BAD=90°,AB=AD=2,∠BAO=∠ABF=45°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴OA=OB=$\sqrt{2}$,
∴△AOB的面积=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{2}$=1,
∵以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,AC⊥BD,
∴O为切点,
∵扇形AOE的面积=$\frac{45π×(\sqrt{2})^{2}}{360}$=$\frac{π}{4}$,扇形ABF的面积=$\frac{45π×{2}^{2}}{360}$=$\frac{π}{2}$,
∴图中阴影部分的面积=$\frac{π}{2}$-(1-$\frac{π}{4}$)=$\frac{3π}{4}$-1;
故选:D.
点评 本题考查了切线的性质、正方形的性质、勾股定理、扇形面积的计算;熟练掌握切线的性质和正方形的性质,求出扇形的面积是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.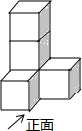 由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )
由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )
 由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )
由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )| A. | 左视图与俯视图相同 | B. | 左视图与主视图相同 | ||
| C. | 主视图与俯视图相同 | D. | 三种视图都相同 |
6. 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为$\sqrt{5}$,则下列结论中正确的是( )
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为$\sqrt{5}$,则下列结论中正确的是( )
 如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为$\sqrt{5}$,则下列结论中正确的是( )
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为$\sqrt{5}$,则下列结论中正确的是( )| A. | m=5 | B. | m=4$\sqrt{5}$ | C. | m=3$\sqrt{5}$ | D. | m=10 |
13. 若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )
若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )
 若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )
若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )| A. | x>2 | B. | x<2 | C. | x>-1 | D. | x<-1 |
10.计算3x3•(-2x2)的结果是( )
| A. | -6x5 | B. | -6x6 | C. | -x5 | D. | x5 |
11.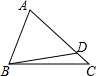 如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
 如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )| A. | AC>BC | B. | AC=BC | C. | ∠A>∠ABC | D. | ∠A=∠ABC |
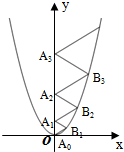 二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2016在y轴的正半轴上,B1,B2,B3,…,B2016 在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2015B2016A2016都为等边三角形,则△A2015B2016A2016的边长=2016.
二次函数y=$\frac{2}{3}$x2的图象如图所示,点A0位于坐标原点,A1,A2,A3,…,A2016在y轴的正半轴上,B1,B2,B3,…,B2016 在二次函数y=$\frac{2}{3}$x2第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2015B2016A2016都为等边三角形,则△A2015B2016A2016的边长=2016. 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: