题目内容
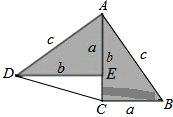 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.考点:勾股定理的证明
专题:
分析:连结DB,过点D作BC边上的高DF,根据S四边形ADCB=S△ACD+S△ABC=S△ADB+S△DCB即可求解.
解答: 证明:连结DB,过点D作BC边上的高DF,则DF=EC=b-a.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=
b2+
ab.
又∵S四边形ADCB=S△ADB+S△DCB=
c2+
a(b-a)
∴
b2+
ab=
c2+
a(b-a)
∴a2+b2=c2
 证明:连结DB,过点D作BC边上的高DF,则DF=EC=b-a.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b-a.∵S四边形ADCB=S△ACD+S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵S四边形ADCB=S△ADB+S△DCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a2+b2=c2
点评:本题考查了用数形结合来证明勾股定理,证明勾股定理常用的方法是利用面积证明,本题锻炼了同学们数形结合的思想方法.

练习册系列答案
相关题目
 如图,△ABC中,AD⊥BC,垂足是D.若BC=14,AD=12,tan∠BAD=
如图,△ABC中,AD⊥BC,垂足是D.若BC=14,AD=12,tan∠BAD= 将连续正整数按图所示的规律排列,观察图表并回答下列问题:
将连续正整数按图所示的规律排列,观察图表并回答下列问题: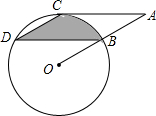 如图,点B、C、D都在⊙O上,过点C的⊙O的切线交OB延长线于点A,C连接CD、BD,若∠CDB=∠OBD=30°,OB=6cm.
如图,点B、C、D都在⊙O上,过点C的⊙O的切线交OB延长线于点A,C连接CD、BD,若∠CDB=∠OBD=30°,OB=6cm.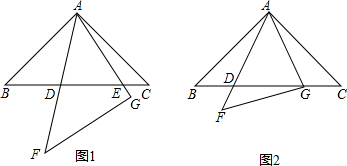
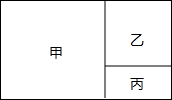 如图,是我市一块长方形土地,政府统一规划,把地分成甲、乙、丙三部分,甲和乙为正方形,现计划甲建设住宅区,乙建设一座标准化的中学,丙地建成植物园,若已知这块地的宽为120米,丙地的面积为3200平方米,请你计算出这块地的长是多少?
如图,是我市一块长方形土地,政府统一规划,把地分成甲、乙、丙三部分,甲和乙为正方形,现计划甲建设住宅区,乙建设一座标准化的中学,丙地建成植物园,若已知这块地的宽为120米,丙地的面积为3200平方米,请你计算出这块地的长是多少?