题目内容
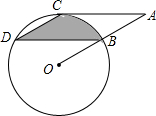 如图,点B、C、D都在⊙O上,过点C的⊙O的切线交OB延长线于点A,C连接CD、BD,若∠CDB=∠OBD=30°,OB=6cm.
如图,点B、C、D都在⊙O上,过点C的⊙O的切线交OB延长线于点A,C连接CD、BD,若∠CDB=∠OBD=30°,OB=6cm.(1)求证:AC∥BD;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
考点:切线的性质,扇形面积的计算
专题:
分析:(1)首先连接OC,交BD于E,由∠CDB=∠OBD=30°,根据圆周角定理,可求得∠BOC=60°,即可得OC⊥BD,又由过点C的⊙O的切线交OB延长线于点A,即可证得AC∥BD;
(2)易证得△CDE≌△OEB(ASA),则可得S阴影=S扇形COB=
=6π.
(2)易证得△CDE≌△OEB(ASA),则可得S阴影=S扇形COB=
| 60×π×62 |
| 360 |
解答: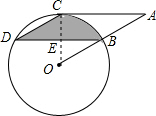 (1)证明:连接OC,交BD于E,
(1)证明:连接OC,交BD于E,
∵∠CDB=∠OBD=30°,
∴∠COB=60°
∴∠OEB=90°.
∵AC是⊙O的切线,
∴∠OCA=90°,
∴∠OCA=∠OEB.
∴AC∥BD;
(2)∵∠OEB=90°,
∴DE=BE,
又∵∠CDB=∠OBD=30°,∠CED=90°,
在△CDE和△OEB中,
,
∴△CDE≌△OEB(ASA),
∴S阴影=S扇形COB=
=6π.
 (1)证明:连接OC,交BD于E,
(1)证明:连接OC,交BD于E,∵∠CDB=∠OBD=30°,
∴∠COB=60°
∴∠OEB=90°.
∵AC是⊙O的切线,
∴∠OCA=90°,
∴∠OCA=∠OEB.
∴AC∥BD;
(2)∵∠OEB=90°,
∴DE=BE,
又∵∠CDB=∠OBD=30°,∠CED=90°,
在△CDE和△OEB中,
|
∴△CDE≌△OEB(ASA),
∴S阴影=S扇形COB=
| 60×π×62 |
| 360 |
点评:此题考查了切线的性质、扇形的面积以及直角三角形的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
与
最接近的整数是( )
| 40 |
| A、5 | B、6 | C、7 | D、8 |
若a>1,化简
-1=( )
| (a-1)2 |
| A、a-2 | B、2-a | C、a | D、-a |
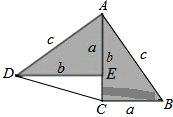 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.△ADE和△ACB是两直角边为a,b,斜边为c的全等的直角三角形,按如图所示摆放,其中∠DAB=90°,求证:a2+b2=c2.