题目内容
6.商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场每天可多售出2件,设每件商品降低x元据此规律,请回答:(1)商场日销售量增加2x件,每件商品盈利50-x元(用含x的代数式表示);
(2)在上述条件不变,销售正常的情况下,设商场日盈利y元,求y与x的函数关系式;
(3)在(2)的条件下,每件商品降价多少元时,商场日盈利最高?
分析 (1)降价1元,可多售出2件,降价x元,可多售出2x件,盈利的钱数=原来的盈利-降低的钱数;
(2)根据日盈利=每件商品盈利的钱数×(原来每天销售的商品件数30+2×降价的钱数),列出函数表达式即可;
(3)求出(2)中函数表达式的顶点坐标的横坐标即可解决问题.
解答 解:(1)降价1元,可多售出2件,降价x元,可多售出2x件,盈利的钱数=50-x,故答案为2x;50-x;
(2)y=(50-x)(30+2x)=-2x2+70x+1500;
(3)y=-2x2+70x+1500,
当x=-$\frac{b}{2a}$=17.5时,y最大.
答:每件商品降价17.5元时,商场日盈利的最大.
点评 此题主要考查了二次函数的应用;得到日盈利的等量关系是解决本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2.回答下列问题:
如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2.回答下列问题: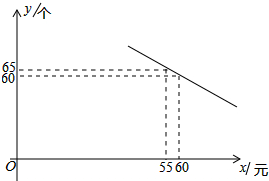 某体育用品商店试销一款成本为50元的排球,规定①试销售期三天;②试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
某体育用品商店试销一款成本为50元的排球,规定①试销售期三天;②试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.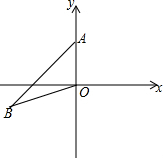 如图,已知A(0,4),点B在第三象限,且∠B=30°
如图,已知A(0,4),点B在第三象限,且∠B=30° 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,CD与AB的延长线相交于点D,∠CAD=20°,则∠D=50°.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,CD与AB的延长线相交于点D,∠CAD=20°,则∠D=50°.