题目内容
3.两组数据:98,99,99,100和98.5,99,99,99.5,则关于以下统计量说法不正确的是( )| A. | 平均数相等 | B. | 中位数相等 | C. | 众数相等 | D. | 方差相等 |
分析 根据平均数的计算公式、众数和中位数的概念以及方差的计算公式计算,判断即可.
解答 解:$\frac{1}{4}$(98+99+99+100)=99,$\frac{1}{4}$(98.5+99+99+99.5)=99,
平均数相等,A不合题意;
两组数据:98,99,99,100和98.5,99,99,99.5的中位数都是99,众数是99,
则中位数相等,众数相等,B、C不合题意;
$\frac{1}{4}$[(98-99)2+(99-99)2+(99-99)2+[100-99)2]=$\frac{1}{2}$,
$\frac{1}{4}$[(98.5-99)2+(99-99)2+(99-99)2+[99.5-99)2]=$\frac{1}{8}$,
方差不相等,D符合题意,
故选:D.
点评 本题考查的是平均数、众数、中位数和方差,掌握它们的概念以及计算公式是解题的关键.

练习册系列答案
相关题目
13.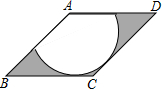 如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
 如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
如图,在菱形ABCD中,∠B=45°,以点A为圆心的扇形与BC,CD相切,向这样一个靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )| A. | 1-$\frac{3\sqrt{2}π}{16}$ | B. | $\sqrt{2}-\frac{3π}{8}$ | C. | 1-$\frac{3π}{8}$ | D. | $\frac{3π}{8}$ |
14.关于x的一元二次方程(m2-1)x2-2(m+1)x+1=0有实数根,则m的取值范围是( )
| A. | m>1 | B. | m≥1 | C. | m≥-1且m≠1 | D. | m>-1且m≠1 |
11.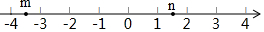 实数m,n在数轴上的对应点的位置如图所示,下列结论正确的是( )
实数m,n在数轴上的对应点的位置如图所示,下列结论正确的是( )
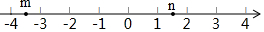 实数m,n在数轴上的对应点的位置如图所示,下列结论正确的是( )
实数m,n在数轴上的对应点的位置如图所示,下列结论正确的是( )| A. | m>-3 | B. | m<-4 | C. | m>n | D. | m<-n |
8.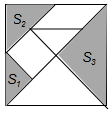 有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
 有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )
有一副七巧板如图所示,其中三个阴影部分的面积分别为S1,S2,S3,则S1:S2:S3=( )| A. | 1:2:3 | B. | 1:$\sqrt{2}$:2 | C. | 1:$\sqrt{2}$:4 | D. | 1:2:4 |
7.巴黎与北京的时差为-7时,如果北京时间是10月26日5:00,那么巴黎时间是( )
| A. | 10月26日12:00 | B. | 10月26日2:00 | C. | 10月25日22:00 | D. | 10月25日12:00 |
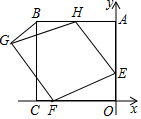 如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH.
如图,在平面直角坐标系中,正方形ABCD的顶点C、A分别在x、y轴上,A(0,6),E(0,2),点H、F分别在边AB、OC上,以H、E、F为顶点作菱形EFGH. 实践与操作:
实践与操作: