题目内容
11．
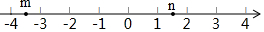实数m，n在数轴上的对应点的位置如图所示，下列结论正确的是（ ）| A． | m＞-3 | B． | m＜-4 | C． | m＞n | D． | m＜-n |
分析 利用数轴上m，n所在的位置，进而得出m，-n的取值范围，进而比较得出答案．
解答 解：A、如图所示：-4＜m＜-3，故此选项错误；
B、如图所示：-4＜m＜-3，故此选项错误；
C、如图所示：-4＜m＜-3，1＜n＜2，故m＜n，故此选项错误；
D、如图所示：-4＜m＜-3，1＜n＜2，则，-2＜n＜-1，故m＜-n，故此选项正确．
故选：D．
点评 此题主要考查了实数与数轴，正确得出m，-n的取值范围是解题关键．
练习册系列答案
相关题目
2．某商场为了迎接“6.1儿童节“，以调低价格的方式促销n个不同的玩具，调整后的单价y（元）与调整前的单价x（元）满足一次函数关系，如表：
当这些玩具调整后的单价都大于2元时，解答下列问题：
（1）y与x的函数关系式为，x的取值范围为；
（2）某个玩具调整前单价是108元，顾客购买这个玩具省了元；
（3）这n个玩具调整前、后的平均单价分别为$\overline{x}$（元）、$\overline{y}$（元），猜想$\overline{y}$与$\overline{x}$的关系式，并写出推导过程．
| 第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
| 调整前单价x （元） | x1 | x2=6 | x3=72 | x4 | … | xn |
| 调整后单价y （元） | y1 | y2=4 | y3=59 | y4 | … | yn |
（1）y与x的函数关系式为，x的取值范围为；
（2）某个玩具调整前单价是108元，顾客购买这个玩具省了元；
（3）这n个玩具调整前、后的平均单价分别为$\overline{x}$（元）、$\overline{y}$（元），猜想$\overline{y}$与$\overline{x}$的关系式，并写出推导过程．
如图，在平行四边形ABCD中，AD=2CD，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论①∠DCF=∠ECF；②EF=CF；③∠DFE=3∠AEF；④S△BEC＜2S△CEF．中一定成立的是②③④．（请填序号）
6．
如图，AB∥CD，AD与BC相交于点E，若∠A=40°，∠C=35°，则∠BED=（ ）
如图，AB∥CD，AD与BC相交于点E，若∠A=40°，∠C=35°，则∠BED=（ ）| A． | 70° | B． | 75° | C． | 80° | D． | 85° |
16．
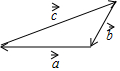如图，已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$，那么下列结论正确的是（ ）
如图，已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$，那么下列结论正确的是（ ）| A． | $\overrightarrow{a}$$+\overrightarrow{b}$=$\overrightarrow{c}$ | B． | $\overrightarrow{b}$$+\overrightarrow{c}$=$\overrightarrow{a}$ | C． | $\overrightarrow{a}$$+\overrightarrow{c}$=$\overrightarrow{b}$ | D． | $\overrightarrow{a}$$+\overrightarrow{c}$=$-\overrightarrow{b}$ |
3．两组数据：98，99，99，100和98.5，99，99，99.5，则关于以下统计量说法不正确的是（ ）
| A． | 平均数相等 | B． | 中位数相等 | C． | 众数相等 | D． | 方差相等 |
如图，已知△ABC内接于⊙O，CD是⊙O的切线与半径OB的延长线交于点D，∠A=30°，求∠BCD的度数．