题目内容
17.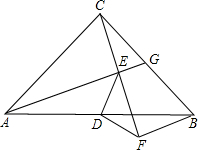 已知等腰Rt△ABC中,∠ACB=90°,AC=BC,点G在BC上,连接AG,过C作CF⊥AG,垂足为点E,过点B作BF⊥CF于点F.
已知等腰Rt△ABC中,∠ACB=90°,AC=BC,点G在BC上,连接AG,过C作CF⊥AG,垂足为点E,过点B作BF⊥CF于点F.(1)求证:△CBF≌△ACE;
(2)若点D是AB的中点,连接DE、DF,求证:DE=DF.
分析 (1)根据垂直的定义和等角的余角相等以及全等三角形的判定证明即可;
(2)根据全等三角形的性质和判定证明即可.
解答 (1)证明:如图,因为AE⊥CF,BF⊥CE,∠ACB=90°,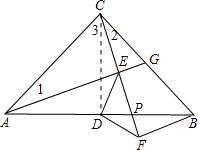 ∴∠1﹢∠3=∠2﹢∠3=90°,
∴∠1﹢∠3=∠2﹢∠3=90°,
∴∠1=∠2,
在△CBF与△ACE中,
$\left\{\begin{array}{l}{∠1=∠2}\\{∠AEC=∠CFB=90°}\\{AC=CB}\end{array}\right.$,
∴△CBF≌△ACE(AAS);
(2)证明:连接CD,
∵△ACE≌△CBF,
∴CE=BF,
∵等腰RT△ABC中,点D是AB的中点,
∴CD=BD,
∵CD⊥BD,
∠DCE+∠DPC=∠FBP+∠FPB=90°,
∴∠DCE=∠DBF,
在△DCE与△DBF中,
$\left\{\begin{array}{l}{CE=BF}\\{∠DCE=∠DBF}\\{CD=BD}\end{array}\right.$,
∴△DCE≌△DBF(SAS),
∴DE=DF.
点评 此题考查全等三角形的判定和性质,关键是根据垂直的定义和等角的余角相等以及全等三角形的判定证明.

练习册系列答案
相关题目
12.如果a2+mab+9b2是一个完全平方式,则m应是( )
| A. | 3 | B. | ±3 | C. | 6 | D. | ±6 |
 如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于E,在AC边上有一点D满足∠CBD=20°,连结DE,求∠CED的度数.
如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于E,在AC边上有一点D满足∠CBD=20°,连结DE,求∠CED的度数.