题目内容
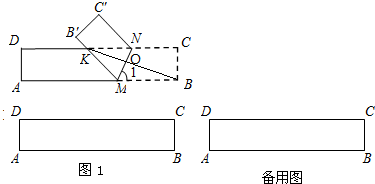
13.如图1,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK,KB交MN于O.(1)若∠1=80°,求∠MKN的度数;
(2)当B与D重合时,画出图形,并求出∠KON的度数;
(3)△MNK的面积能否小于$\frac{1}{2}$?若能,求出此时∠1的度数;若不能,试说明理由.
分析 (1)由平行线的性质可知∠KNM=∠1,由翻折的性质可知:KMN=∠1=80°,最后依据三角形的内角和定理可求得∠MKN的值;
(2)先根据题意画出图形,然后由翻折的性质可知DO=BO.接下来依据AAS证明△DON≌△BOM(AAS),由全等三角形的性质可知DN=BM,根据有一组对边平行且相等的四边形是平行四边形证明四边形DMBN是平行四边形,然后根据DM=BM可知平行四边形DMBN是菱形,故此BD⊥MN从而得到∠KON=90°;
(3)过M点作ME⊥DN,垂足为E,先证明KN=KM,然后利用矩形的面积公式计算即可.
解答 解:(1)∵四边形ABCD是矩形,
∴AM∥DN.
∴∠KNM=∠1.
∵∠1=80°,
∴∠KNM=∠KMN=∠1=80°.
∴∠MKN=20°.
(2)当B与D重合时,如图所示,K、B、D三点重合,连接NB.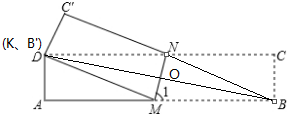
∵B、D关于MN对称,
∴DO=BO.
在△DON和△BOM中,
$\left\{\begin{array}{l}{∠DNM=∠1}\\{∠NOD=∠MOB}\\{DO=BO}\end{array}\right.$,
∴△DON≌△BOM(AAS).
∴DN=BM.
∵DC∥AB,
∴四边形DMBN是平行四边形.
∵DM=BM,
∴平行四边形DMBN是菱形.
∴BD⊥MN.
∴∠DON=90°即∠KON=90°.
(3)能.
过M点作ME⊥DN,垂足为E,则ME=AD=1.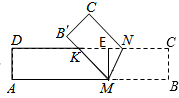
∵∠KNM=∠KMN,
∴MK=NK,
又∵MK≥ME,
∴NK≥1.
∴△MNK的面积=$\frac{1}{2}$NK•ME≥$\frac{1}{2}$
∴△MNK的面积不可能小于$\frac{1}{2}$.
点评 本题主要考查的是翻折的性质、菱形的判定,证得四边形DMBN是菱形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.不等式5-3x≥2x-6的非负整数解有( )个.
| A. | 4 | B. | 3 | C. | 5 | D. | 6 |
8.数轴上与原点距离小于3.5个单位长度的整数点的个数是( )
| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
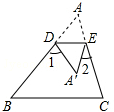 如图,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED内部A′处,已知∠A=40°,则∠1+∠2=80°度.
如图,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED内部A′处,已知∠A=40°,则∠1+∠2=80°度.