题目内容
5.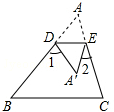 如图,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED内部A′处,已知∠A=40°,则∠1+∠2=80°度.
如图,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE折叠,使点A落在四边形BCED内部A′处,已知∠A=40°,则∠1+∠2=80°度.
分析 根据平角定义和折叠的性质,得∠1+∠2=360°-2(∠ADE+∠AED),再利用三角形的内角和定理进行转换,得∠1+∠2=360°-2(180°-∠A)=2∠A.
解答 解:根据平角的定义和折叠的性质,得
∠1+∠2=360°-2(∠ADE+∠AED),
又∵∠ADE+∠AED=180°-∠A,
∴∠1+∠2=360°-2(180°-∠A)=2∠A=80°.
故答案为:80°.
点评 本题主要考查了三角形的内角和定理,平角的定义、折叠的性质,综合运用各定理是解答此题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
14.在二次根式$\sqrt{2x-6}$中,x的取值范围是( )
| A. | x>3 | B. | x≥3 | C. | x≤3 | D. | x<3 |
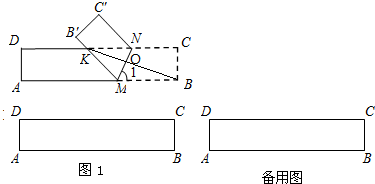
 在△ABC中,AB=AC,AE=AD,且BD与CE交于点O,连AO延长交BC于F,求证:
在△ABC中,AB=AC,AE=AD,且BD与CE交于点O,连AO延长交BC于F,求证: