题目内容
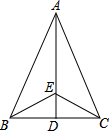 如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,若点E是AD上的任意一点,连接BE、CE,试探求∠EBD与∠ECD的大小关系,并说明理由.
如图,在△ABC中,AB=AC,AD是∠BAC的角平分线,若点E是AD上的任意一点,连接BE、CE,试探求∠EBD与∠ECD的大小关系,并说明理由.考点:等腰三角形的性质
专题:
分析:由条件可知BD=DC,且AD⊥BC,则AD为BC的垂直平分线,则EB=EC,可知∠EBD=∠ECD.
解答:解:∠EBD=∠ECD,理由如下:
∵AB=AC,AD是∠BAC的角平分线,
∴BD=DC,AD⊥BC,
∴AD为BC的垂直平分线,
∵点E在AD上,
∴EB=EC,
∴∠EBD=∠ECD.
∵AB=AC,AD是∠BAC的角平分线,
∴BD=DC,AD⊥BC,
∴AD为BC的垂直平分线,
∵点E在AD上,
∴EB=EC,
∴∠EBD=∠ECD.
点评:本题主要考查等腰三角形的性质,由条件得出AD为BC的垂直平分线是解题的关键.

练习册系列答案
相关题目
下列函数中,y随x的增大而减小的是( )
| A、y=-3x | ||
| B、y=3x-4 | ||
C、y=-
| ||
D、y=
|
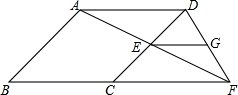 如图,在菱形ABCD中,E是CD上的一点,连接AE并延长交BC于点F,连接DF,过点E作EG∥BF交DF于点G.试探究EC与EG的大小关系.
如图,在菱形ABCD中,E是CD上的一点,连接AE并延长交BC于点F,连接DF,过点E作EG∥BF交DF于点G.试探究EC与EG的大小关系.