题目内容
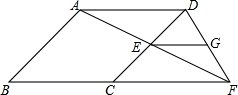如图，在菱形ABCD中，E是CD上的一点，连接AE并延长交BC于点F，连接DF，过点E作EG∥BF交DF于点G．试探究EC与EG的大小关系．考点：菱形的性质,相似三角形的判定与性质
专题：
分析：求出△ADF和△EGF相似，根据相似三角形对应边成比例可得
=
，再求出△ADE和△FCE相似，根据相似三角形对应边成比例可得
=
，然后求出
=
，再根据菱形的四条边都相等可得AD=CD，即可得解．
| EG |
| AD |
| EF |
| AF |
| CE |
| DE |
| EF |
| AE |
| CE |
| CD |
| EF |
| AF |
解答：解：∵EG∥BF，
∴△ADF∽△EGF，
∴
=
，
∵菱形对边AD∥BC，
∴△ADE∽△FCE，
∴
=
，
∴
=
，
∴
=
，
在菱形ABCD中，AD=CD，
∴CE=EG．
∴△ADF∽△EGF，
∴
| EG |
| AD |
| EF |
| AF |
∵菱形对边AD∥BC，
∴△ADE∽△FCE，
∴
| CE |
| DE |
| EF |
| AE |
∴
| CE |
| CD |
| EF |
| AF |
∴
| CE |
| CD |
| EG |
| AD |
在菱形ABCD中，AD=CD，
∴CE=EG．
点评：本题考查了菱形的性质，相似三角形的判定与性质，熟记性质并确定出相似三角形是解题的关键．
练习册系列答案
相关题目
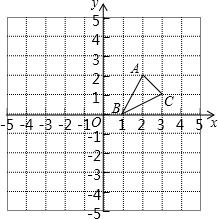如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，三个顶点的坐标分别为A（2，2），B（1，0），C（3，1）
如图，直线AB、CD相交于O点，若∠COE=∠FOB=90°，∠AOC=30°，则∠EOF=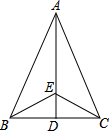
如图，在△ABC中，AB=AC，AD是∠BAC的角平分线，若点E是AD上的任意一点，连接BE、CE，试探求∠EBD与∠ECD的大小关系，并说明理由．