题目内容
 如图两射线表示某电信公司提供两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,当通话时间为100分钟,两种方案通讯费用相差20元;当通话时间为180分钟,两种方案通讯费用一样;当两种方案通讯费用相差40元时,则通话时间为
如图两射线表示某电信公司提供两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,当通话时间为100分钟,两种方案通讯费用相差20元;当通话时间为180分钟,两种方案通讯费用一样;当两种方案通讯费用相差40元时,则通话时间为考点:一次函数的应用
专题:
分析:根据已知假设出两一次函数解析式,进而得出两函数的系数之间的关系,进而得出当k1-k2=-
,b=-45时或当k2-k1=-
,b=45时,分别求出即可.
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:设两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系分别为:y1=k1x,y2=k2x+b,
∵当通话时间为100分钟,两种方案通讯费用相差20元;
∴y1-y2=k1x-(k2x+b)=100(k1-k2)-b=20或y2-y1=k2x+b-k1x=100(k2-k1)+b=20;
∵当通话时间为180分钟,两种方案通讯费用一样;
∴y1-y2=k1x-(k2x+b)=180(k1-k2)-b=0也可以写为:180(k2-k1)+b=0
∴
或
,
解得:
或
,
∵当两种方案通讯费用相差40元时,
∴y1-y2=k1x-(k2x+b)=x(k1-k2)-b=40或y2-y1=k2x+b-k1x=x(k2-k1)+b=40;
∴当k1-k2=-
,b=-45时,
x(k1-k2)-b=40,
x×(-
)+45=40,
解得:x=20,
当k2-k1=-
,b=45时,
∴(k1-k2)=
,
x(k1-k2)-b=40,
x×
-45=40,
解得:x=340,
故答案为:20或340.
∵当通话时间为100分钟,两种方案通讯费用相差20元;
∴y1-y2=k1x-(k2x+b)=100(k1-k2)-b=20或y2-y1=k2x+b-k1x=100(k2-k1)+b=20;
∵当通话时间为180分钟,两种方案通讯费用一样;
∴y1-y2=k1x-(k2x+b)=180(k1-k2)-b=0也可以写为:180(k2-k1)+b=0
∴
|
|
解得:
|
|
∵当两种方案通讯费用相差40元时,
∴y1-y2=k1x-(k2x+b)=x(k1-k2)-b=40或y2-y1=k2x+b-k1x=x(k2-k1)+b=40;
∴当k1-k2=-
| 1 |
| 4 |
x(k1-k2)-b=40,
x×(-
| 1 |
| 4 |
解得:x=20,
当k2-k1=-
| 1 |
| 4 |
∴(k1-k2)=
| 1 |
| 4 |
x(k1-k2)-b=40,
x×
| 1 |
| 4 |
解得:x=340,
故答案为:20或340.
点评:此题主要考查了一次函数的应用,根据已知得出两函数之间系数之间关系进而求出是解题关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 如图,D为△ABC的BC边的中点,E为AC边上的一点,AC=3CE,BE和AD交于G点,则AG:GD=( )
如图,D为△ABC的BC边的中点,E为AC边上的一点,AC=3CE,BE和AD交于G点,则AG:GD=( )| A、2 | B、3 | C、3或4 | D、4 |
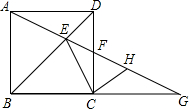 如图所示,在正方形ABCD中,点F在CD边上,射线AF交BD于点E,交BC的延长线于点G.求证:
如图所示,在正方形ABCD中,点F在CD边上,射线AF交BD于点E,交BC的延长线于点G.求证: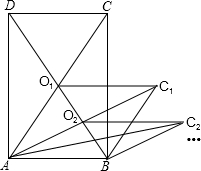 如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两边邻作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABC7O7的面积为
如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB、AO1为两边邻作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB、AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABC7O7的面积为