题目内容
11.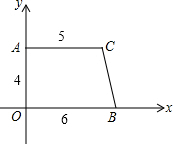 如图,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,
如图,在直角梯形AOBC中,AC平行于OB,且OB=6,AC=5,OA=4,(1)求出经过B、C两点的直线的解析式:
(2)在边AC和BC(含端点)上分别找到点M和点N,使得△MON的面积最大,并说明理由.
(3)在(2)成立的条件下,是否存在M和N,同时满足△MON的周长还是短?若存在,请求出周长的最小值,并求出此时点M、N的坐标:若不存在,请说明理由.
分析 (1)由OB=6,点B在x轴,得到B点的坐标,根据AC∥OB,AC=5,得到点C的坐标,再用待定系数法即可得出结论;
(2)过点M作MP∥OA,交ON于点P,过点N作NQ∥OB,分别交OA、MP于两点Q、G,则S△MON=S△OMP+S△NMP=$\frac{1}{2}$MP•QG+$\frac{1}{2}$MP•NG=$\frac{1}{2}$MP•QN,因为QN取得最大值是QN=OB时,△MON的面积最大值=$\frac{1}{2}$OA•OB,
(3)设O关于AC的对称点D,连接DB,交AC于M,此时△OMN面积最大,周长最小.
解答 解:(1)∵OB=6,OA=4,
∴B(6,0),
∵AC∥OB,AC=5,
∴C(5,4),
设直线BC解析式为y=kx+b,
∴$\left\{\begin{array}{l}{6k+b=0}\\{5k+b=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-4}\\{b=24}\end{array}\right.$,
∴直线BC解析式为y=-4x+24;
(2)如图,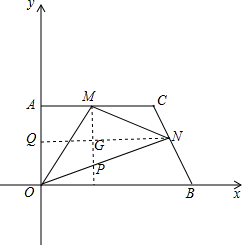
过点M作MP∥OA,交ON于点P,过点N作NQ∥OB,分别交OA、MP于两点Q、G,
则S△MON=S△OMP+S△NMP=$\frac{1}{2}$MP•QG+$\frac{1}{2}$MP•NG=$\frac{1}{2}$MP•QN,
∵MP≤OA,QN≤OB,
∴当点N与点B重合,QN取得最大值OB时,△MON的面积最大值=$\frac{1}{2}$OA•OB(点M在线段AC上任意一点),
(3)如图1,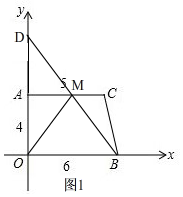
由(2)知,点N和B重合,即:N(6,0),
设O关于AC的对称点D,连接DB,交AC于M,
此时△MON的面积最大,周长最短,
∵AM∥BO
∴$\frac{AD}{OD}=\frac{AM}{OB}$,即$\frac{4}{8}=\frac{AM}{6}$,
∴AM=3,
∴M(3,4).
点评 此题是四边形综合题,主要考查了直角梯形的性质,待定系数法,坐标和图形的性质,轴对称的性质等,作出辅助线是本题的关键.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | 3,4,8 | B. | 5,6,11 | C. | 5,6,10 | D. | 1,2,3 |
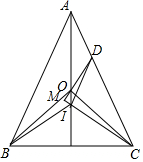 △ABC中,AB=AC,O、I分别是其外心、内心,点D在AC上,且DI∥AB,DO的延长线交CI的延长线于M.求证:DM⊥CM.
△ABC中,AB=AC,O、I分别是其外心、内心,点D在AC上,且DI∥AB,DO的延长线交CI的延长线于M.求证:DM⊥CM. 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:
如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论: