题目内容
 如图,△ABC三边的中点分别是D、E、F,某同学随机地把一滴颜料滴在△ABC内,则这滴颜料落在△BEF内的概率是( )
如图,△ABC三边的中点分别是D、E、F,某同学随机地把一滴颜料滴在△ABC内,则这滴颜料落在△BEF内的概率是( )A、
| ||
B、
| ||
C、
| ||
| D、无法确定 |
考点:几何概率
专题:
分析:利用三角形中位线的性质与判定得出EF,ED,DF分别是△ABC的中位线,进而得出S△AED=S△BEF=S△CDF=S△EFD,进而得出答案.
解答:解:∵△ABC三边的中点分别是D、E、F,
∴DE∥BC,EF∥AC,FD∥AB,且EF,ED,DF分别是△ABC的中位线,
∴S△AED=S△BEF=S△CDF=
S△ABC,
∴S△AED=S△BEF=S△CDF=S△EFD,
∴某同学随机地把一滴颜料滴在△ABC内,则这滴颜料落在△BEF内的概率是:
.
故选:B.
∴DE∥BC,EF∥AC,FD∥AB,且EF,ED,DF分别是△ABC的中位线,
∴S△AED=S△BEF=S△CDF=
| 1 |
| 4 |
∴S△AED=S△BEF=S△CDF=S△EFD,
∴某同学随机地把一滴颜料滴在△ABC内,则这滴颜料落在△BEF内的概率是:
| 1 |
| 4 |
故选:B.
点评:此题主要考查了几何概率,熟练利用三角形中位线定理是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
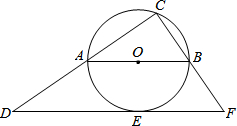 如图,AB为⊙O的直径,C为⊙O上一点,DF切⊙O于E点,分别与CA、CB的延长线于点D、F,已知AB∥DF,CD=4,CF=3,则AC=( )
如图,AB为⊙O的直径,C为⊙O上一点,DF切⊙O于E点,分别与CA、CB的延长线于点D、F,已知AB∥DF,CD=4,CF=3,则AC=( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知不等式组
,则化简|4x+5|-|x-1|的结果为( )
|
| A、3x+4 | B、3x+6 |
| C、5x+4 | D、5x+6 |
 如图,反比例函数y=
如图,反比例函数y= 已知关于x一元二次方程x2-2(k+1)x+k2-2k-3=0有两个不相等的实数根
已知关于x一元二次方程x2-2(k+1)x+k2-2k-3=0有两个不相等的实数根 在正方形网格中建立如图的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在正方形网格中建立如图的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题: