题目内容
17.设不等式ax2+5x+b>0的解集是(2,3),求不等式bx2+5x+a>0的解集.分析 根据所给的一元二次不等式的解集,写出对应的一元二次方程的解,根据根与系数的关系得到不等式的系数的值,解出一元二次不等式得到解集.
解答 解:∵不等式ax2-5x+b>0的解集是2<x<3
∴ax2+5x+b=0的解是x=3,x=2
∴$\frac{-5}{a}$=5,$\frac{b}{a}$=6
∴a=-1,b=-6,
不等式bx2+5x+a>0,即-6x2+5x-1>0,
∴6x2-5x+1<0,
∴(2x-1)(3x-1)<0,
解得:$\frac{1}{3}$<x<$\frac{1}{2}$
∴不等式的解集是$\frac{1}{3}$$<x<\frac{1}{2}$.
点评 本题考查根与系数的关系及一元二次方程和一元二次不等式的关系,本题解题的关键是根据所给的不等式的解集得到对应的方程的解,根据根与系数的关系得到结果.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
7.下列说法中正确的是( )
| A. | 平分弦的直径平分弦所对的弧 | |
| B. | 圆内接正六边形,一条边所对的圆周角是30° | |
| C. | 相等的圆周角所对的弧也相等 | |
| D. | 若两条平行直线被一个圆截得的线段长度相等,则圆心到这两条直线的距离相等 |
9.已知一元二次方程ax2+c=0(a≠0),若方程有解,则必须有c等于( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 不能确定 |
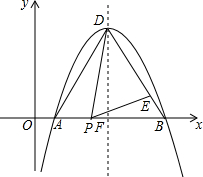 已知,在平面直角坐标系中,二次函数y=-$\frac{4}{9}$(x-4)2+4与x轴交于A、B两点,D为抛物线的顶点,对称轴与x轴交于点F,E为BD上一点,且BE:BD=1:5,P为AB上一点,且∠DPE=∠DAB,求P点坐标.
已知,在平面直角坐标系中,二次函数y=-$\frac{4}{9}$(x-4)2+4与x轴交于A、B两点,D为抛物线的顶点,对称轴与x轴交于点F,E为BD上一点,且BE:BD=1:5,P为AB上一点,且∠DPE=∠DAB,求P点坐标. 如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC于E,连结OE,若CD=$\sqrt{3}$.∠ACB=30°,则DE=$\frac{\sqrt{3}}{2}$,OE=$\frac{\sqrt{7}}{2}$.
如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC于E,连结OE,若CD=$\sqrt{3}$.∠ACB=30°,则DE=$\frac{\sqrt{3}}{2}$,OE=$\frac{\sqrt{7}}{2}$. 如图,四边形ABCD和四边形ECGF都是正方形,M,N分别是线段BE和GD的中点,判断△CMN的形状,并说明理由.
如图,四边形ABCD和四边形ECGF都是正方形,M,N分别是线段BE和GD的中点,判断△CMN的形状,并说明理由.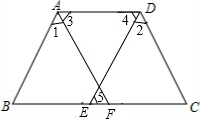 如图,已知∠1=∠2,∠4=∠5,∠3=∠C,求证:AB∥DE.
如图,已知∠1=∠2,∠4=∠5,∠3=∠C,求证:AB∥DE.