题目内容
18. 如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形),则$\frac{y}{x}$的值为( )
如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形),则$\frac{y}{x}$的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |
分析 利用拼图前后的面积相等,可列:[(x+y)+y]y=(x+y)2,整理即可得到答案.
解答 解:如图:
由拼图前后的面积相等得:[(x+y)+y]y=(x+y)2,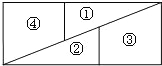
可得:x2+xy-y2=0,
因为y≠0,再除以y2得到($\frac{x}{y}$)2+$\frac{x}{y}$-1=0,
解得:$\frac{x}{y}$=$\frac{\sqrt{5}-1}{2}$或$\frac{x}{y}$=$\frac{-\sqrt{5}-1}{2}$(负值不合题意,舍去).
故选:A.
点评 本题主要考查图形的剪拼,考查学生动手能力.关键是正确拼出图形,掌握图形的面积不变.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
9. 如图,其主视图是( )
如图,其主视图是( )
 如图,其主视图是( )
如图,其主视图是( )| A. |  | B. |  | C. |  | D. | 无法确定 |
8.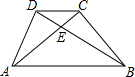 如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )
如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )
 如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )
如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )| A. | 1:9 | B. | 1:4 | C. | 1:3 | D. | 9:1 |
 如图,根据图形,计算∠1=120°.
如图,根据图形,计算∠1=120°.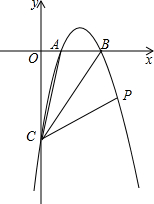 如图,抛物线y=-x2+3x-2与x轴交于A、B两点,与y轴交于C点,点P在抛物线上,∠ACB=∠BCP,求P点的坐标.
如图,抛物线y=-x2+3x-2与x轴交于A、B两点,与y轴交于C点,点P在抛物线上,∠ACB=∠BCP,求P点的坐标.