题目内容
6.下列说法正确的有3个.(1)两条边对应相等的两个直角三角形全等.
(2)有一锐角和斜边对应相等的两直角三角形全等.
(3)一条直角边和一个锐角对应相等的两直角三角形全等.
(4)面积相等的两个直角三角形全等.
分析 利用全等三角形的判定方法逐个判断即可.
解答 解:
(1)当这两条边都是直角边时,结合直角相等,则可用SAS可判定两个三角形全等,当这两条边一条是斜边一条是直角边时,可用HL判定这两个直角三角形全等,故(1)正确;
(2)有一锐角和斜边对应相等时,结合直角,可用AAS来判定这两个直角三角形全等,故(2)正确;
(3)当一条直角边和一个锐角对应相等时,结合直角,可用AAS或ASA来证明这两个直角三角形全等,故(3)正确;
(4)当两个三角形面积相等时,这两个直角三角形不一定会等,故(4)不正确;
综上可知正确的有3个,
故答案为:3.
点评 本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
17.绝对值大于$\frac{11}{5}$而不大于$\frac{11}{2}$的所有整数的积以及和分别等于( )
| A. | 60和12 | B. | -60和0 | C. | 3600和12 | D. | -3600和0 |
11.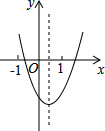 二次函数y=ax2+bx+c的图象如图所示,在ab、ac、b2-4ac,2a+b,a+b+c,0.25a+0.5b+c,a-b+c,这七个代数式中,其值一定是正数的有( )
二次函数y=ax2+bx+c的图象如图所示,在ab、ac、b2-4ac,2a+b,a+b+c,0.25a+0.5b+c,a-b+c,这七个代数式中,其值一定是正数的有( )
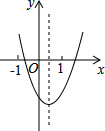 二次函数y=ax2+bx+c的图象如图所示,在ab、ac、b2-4ac,2a+b,a+b+c,0.25a+0.5b+c,a-b+c,这七个代数式中,其值一定是正数的有( )
二次函数y=ax2+bx+c的图象如图所示,在ab、ac、b2-4ac,2a+b,a+b+c,0.25a+0.5b+c,a-b+c,这七个代数式中,其值一定是正数的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18. 如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形),则$\frac{y}{x}$的值为( )
如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形),则$\frac{y}{x}$的值为( )
 如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形),则$\frac{y}{x}$的值为( )
如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形),则$\frac{y}{x}$的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |
 如图,一只蚂蚁从A地到C地,所行的路程x应满足1<x<7.
如图,一只蚂蚁从A地到C地,所行的路程x应满足1<x<7.