题目内容
10．下列二次根式中，属于最简二次根式的是（ ）| A． | $\sqrt{12}$ | B． | $\sqrt{\frac{a}{3}}$ | C． | $\sqrt{a^4}$ | D． | $\sqrt{{x^2}-{y^2}}$ |
分析 根据最简二次根式的定义，可得答案．
解答 解：A、被开方数含开得尽的因数，故A错误；
B、被开方数含分母，故B错误；
C、被开方数含开的尽的因式，故C错误；
D、被开方数不含开得尽的因数或因式，被开方数不含分母，故D正确；
故选：D．
点评 本题考查了最简二次根式，被开方数不含开得尽的因数或因式，被开方数不含分母是判定最简二次根式的条件．
练习册系列答案
相关题目
20．已知点M到x轴、y轴的距离分别为4和6，且点M在x轴的上方、y轴的左侧，则点M的坐标为（ ）
| A． | （4，-6） | B． | （-4，6） | C． | （6，-4） | D． | （-6，4） |
1．在函数y=$\sqrt{x+2}$中，自变量x的取值范围是（ ）
| A． | x≥2 | B． | x≥-2 | C． | x＞2 | D． | x＞-2 |
18．
如图，C是线段AB上任意一点，D是线段AC的中点，E是线段BC的中点，下列说法中错误的是（ ）
如图，C是线段AB上任意一点，D是线段AC的中点，E是线段BC的中点，下列说法中错误的是（ ）| A． | AD+CE=DE | B． | $DE=\frac{1}{2}AB$ | C． | CD=BD-2CE | D． | AD=2BE |
19．在分数$\frac{3}{8}$，$\frac{9}{4}$，$\frac{4}{25}$，$\frac{9}{24}$，$\frac{81}{12}$，$\frac{51}{17}$中，最简分数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
20．
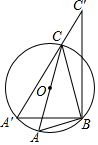在半径为7的圆O中，AC为其直径，点B是圆上的定点，∠ACB=30°，点A′在$\widehat{AC}$上运动（不与A，C重合），C′B⊥A′B交A′C的延长线于点C′，则BC′最大值为 （ ）
在半径为7的圆O中，AC为其直径，点B是圆上的定点，∠ACB=30°，点A′在$\widehat{AC}$上运动（不与A，C重合），C′B⊥A′B交A′C的延长线于点C′，则BC′最大值为 （ ）| A． | 14 | B． | 21 | C． | 14$\sqrt{3}$ | D． | 21$\sqrt{3}$ |