题目内容
 如图是二次函数y=-x2+bx+c的图象,根据图象在横线上填写正确答案.
如图是二次函数y=-x2+bx+c的图象,根据图象在横线上填写正确答案.(1)关于x的一元二次方程-x2+bx+c=0的解是
(2)二次函数的解析式是
(3)关于x的不等式-x2+bx+c>0的解集是
考点:二次函数与不等式(组),抛物线与x轴的交点
专题:
分析:(1)根据二次函数的对称性求出抛物线与x轴的另一交点,然后写出即可;
(2)根据对称轴求出b,再把点(3,0)代入求出c,然后写出解析式即可;
(3)根据函数图象写出x轴上方部分的x的取值范围即可.
(2)根据对称轴求出b,再把点(3,0)代入求出c,然后写出解析式即可;
(3)根据函数图象写出x轴上方部分的x的取值范围即可.
解答:解:(1)∵抛物线对称轴为直线x=1,与x轴的一个交点为(3,0),
∴与x轴的另一个交点为(-1,0),
∴方程的解是x1=-1,x2=3;
(2)对称轴为直线x=-
=1,
解得b=2,
将点(3,0)代入得,-9+3×2+c=0,
解得c=3,
所以,y=-x2+2x+3;
(3)由图可知,不等式-x2+bx+c>0的解集是-1<x<3.
故答案为:(1)x1=-1,x2=3;(2)y-x2+2x+3;(3)-1<x<3.
∴与x轴的另一个交点为(-1,0),
∴方程的解是x1=-1,x2=3;
(2)对称轴为直线x=-
| b |
| 2×(-1) |
解得b=2,
将点(3,0)代入得,-9+3×2+c=0,
解得c=3,
所以,y=-x2+2x+3;
(3)由图可知,不等式-x2+bx+c>0的解集是-1<x<3.
故答案为:(1)x1=-1,x2=3;(2)y-x2+2x+3;(3)-1<x<3.
点评:本题考查了二次函数与不等式,抛物线与x轴的交点问题,解题的关键在于利用对称性求出抛物线与x轴的另一个交点坐标.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
| A、3、4、5 |
| B、6、8、10 |
| C、1、2、3 |
| D、5、12、13 |
2014年11月1日河北省18座大型水库共蓄水22.06亿立方米,比10月1日多蓄水0.97亿立方米,则10月1日这18座大型水库共蓄水( )
| A、23.03亿立方米 |
| B、21.19亿立方米 |
| C、21.11亿立方米 |
| D、21.09亿立方米 |
平面上有任意四点,经过其中两点画一条直线,共可画( )
| A、1条直线 |
| B、6条直线 |
| C、6条或4条直线 |
| D、1条或4条或6条直线 |
 如图,∠AOB=∠COD=90°,OC平分∠AOB,∠DOE:∠BOE=2:3,试求∠COE的度数.
如图,∠AOB=∠COD=90°,OC平分∠AOB,∠DOE:∠BOE=2:3,试求∠COE的度数. 按要求画图:
按要求画图: 随着生活质量的提高,人们的健康意识逐渐增强,安装静水设备的百姓家庭越来越多,某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示,今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
随着生活质量的提高,人们的健康意识逐渐增强,安装静水设备的百姓家庭越来越多,某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示,今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.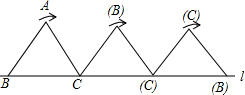 如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为
如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为