题目内容
下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )
| A、3、4、5 |
| B、6、8、10 |
| C、1、2、3 |
| D、5、12、13 |
考点:勾股定理的逆定理
专题:
分析:由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
解答:解:A、32+42=52,故能构成直角三角形;
B、62+82=102,故能构成直角三角形;
C、12+22≠32,故不能构成直角三角形;
D、52+122=132,故能构成直角三角形.
故选:C.
B、62+82=102,故能构成直角三角形;
C、12+22≠32,故不能构成直角三角形;
D、52+122=132,故能构成直角三角形.
故选:C.
点评:本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
下列各组图形中,一定全等的是( )
| A、各有一个角是45°的两个等腰三角形 |
| B、两个等边三角形 |
| C、各有一个角是40°,腰长3cm的两个等腰三角形 |
| D、腰和顶角对应相等的两个等腰三角形 |
某市举行一次少年围棋比赛,各年龄组的参赛人数如下表所示,则全体参赛选手年龄的中位数为( )
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 5 | 19 | 12 | 14 |
| A、13岁 | B、14岁 |
| C、15岁 | D、16岁 |
二次根式
有意义,则x的取值范围是( )
| x-5 |
| A、x>5 | B、x<5 |
| C、x≤5 | D、x≥5 |
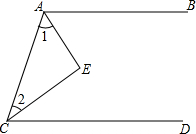 如图,AE平分∠BAC,CE平分∠ACD,要使AB∥CD,则∠1和∠2应满足的条件是
如图,AE平分∠BAC,CE平分∠ACD,要使AB∥CD,则∠1和∠2应满足的条件是 如图是二次函数y=-x2+bx+c的图象,根据图象在横线上填写正确答案.
如图是二次函数y=-x2+bx+c的图象,根据图象在横线上填写正确答案.