题目内容
7. 如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k(k≠0)的图象过点P交x轴于点Q.
如图,二次函数的图象与x轴相交于点A(-3,0)、B(-1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx-4k(k≠0)的图象过点P交x轴于点Q.(1)求该二次函数的解析式;
(2)当点P的坐标为(-4,m)时,求证:∠OPC=∠AQC;
(3)点M、N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M、N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.
①连接AN,当△AMN的面积最大时,求t的值;
②线段PQ能否垂直平分线段MN?如果能,请求出此时直线PQ的函数关系式;如果不能请说明你的理由.
分析 (1)利用交点式求出抛物线的解析式;
(2)证明四边形POQC是平行四边形,则结论得证;
(3)①求出△AMN面积的表达式,利用二次函数的性质,求出△AMN面积最大时t的值.注意:由于自变量取值范围的限制,二次函数并不是在对称轴处取得最大值;
②直线PQ上的点到∠AQC两边的距离相等,则直线PQ能平分∠AQC,所以直线PQ能垂直平分线段MN.
解答 解:(1)设抛物线的解析式为:y=a(x+3)(x+1),
∵抛物线经过点C(0,3),
∴3=a×3×1,解得a=1,
∴抛物线的解析式为:y=(x+3)(x+1)=x2+4x+3;
(2)证明:当x=-4时,y=3,
∴P(-4,3),
∵C(0,3),
∴PC=4且PC∥x轴,
∵一次函数y=kx-4k(k≠0)的图象交x轴于点Q,当y=0时,x=4,
∴Q(4,0),即OQ=4,
∴PC=OQ,又∵PC∥x轴,
∴四边形POQC是平行四边形,
∴∠OPC=∠AQC;
(3)①过点N作ND⊥x轴于点D,则ND∥y轴.
∴△QND∽△QCO
∴$\frac{ND}{CO}$=$\frac{NQ}{CQ}$,
在Rt△OCQ中,
CQ=$\sqrt{CO2+OQ2}$=$\sqrt{32+42}$=5,
∴$\frac{ND}{3}$=$\frac{5-t}{5}$,
∴ND=$\frac{3}{5}$(5-t),
∴S△AMN=$\frac{1}{2}$AM•ND=$\frac{1}{2}$•3t•$\frac{3}{5}$(5-t)=-$\frac{9}{10}$ (t-$\frac{5}{2}$)2+$\frac{48}{5}$,
∵0≤x≤$\frac{7}{3}$,
∴当t=$\frac{7}{3}$时,△AMN的面积最大;
②能.假设PQ垂直平分线段MN,则QM=NQ,
∴7-3t=5-t,
∴t=1.此时AM=3,
即点M与点O重合,QM=NQ=4.
如图,设PQ交y轴于点E,
∵∠MND=90°-∠NMD=∠MQE,
∴Rt△MND∽Rt△EQM,
∴$\frac{ND}{MD}$=$\frac{MQ}{ME}$.
∵ND=$\frac{12}{5}$,DQ=$\frac{16}{5}$,
∴MD=$\frac{4}{5}$,∴MD=$\frac{4}{3}$.
∴E(0,$\frac{4}{3}$),
∵Q(4,0),
∴直线QE为y=-$\frac{1}{3}$x+$\frac{4}{3}$.
即直线PQ为y=-$\frac{1}{3}$x+$\frac{4}{3}$.
点评 本题是二次函数综合题型,考查了二次函数的图象与性质、待定系数法、一次函数、相似三角形、平行四边形、角平分线的性质、二次函数的最值等知识点.试题难度不大,需要注意的是(3)①问中,需要注意在自变量取值区间上求最大值,而不能机械地套用公式.

| A. | 跳远 | B. | 跳高 | C. | 掷铅球 | D. | 掷标枪 |
| 应试者 | 计算机技能 | 语言表达 | 商品知识 |
| 甲 | 70 | 50 | 80 |
| 乙 | 90 | 75 | 45 |
| 丙 | 50 | 60 | 85 |
(2)若商场需要招聘电脑收银员,计算机技能、语言表达和商品知识成绩分别占50%、30%、20%,计算这三名应试者的平均成绩.从成绩看,应该录取谁?
| 甲组 | 173 | 172 | 174 | 172 | 174 |
| 乙组 | 173 | 174 | 172 | 173 | 173 |
| 众数(单位:厘米) | 平均数(单位:厘米) | 方差(单位:厘米) | |
| 甲组 | 172 | 173 | 0.8 |
| 乙组 | 173 | 173 | 0.4 |
 一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:(1)摩托车比汽车晚到1h;(2)A,B两地的路程为20km;(3)摩托车的速度为45km/h,汽车的速度为60km/h;(4)汽车出发1小时候与摩托车相遇,此时距B地40千米;(5)相遇前摩托车的速度比汽车的速度慢.其中正确结论的个数是( )
一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:(1)摩托车比汽车晚到1h;(2)A,B两地的路程为20km;(3)摩托车的速度为45km/h,汽车的速度为60km/h;(4)汽车出发1小时候与摩托车相遇,此时距B地40千米;(5)相遇前摩托车的速度比汽车的速度慢.其中正确结论的个数是( )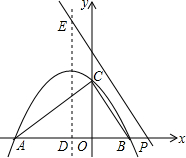 如图,二次函数y=ax2+bx+3的图象抛物线与其对称轴交于点(-1,m),与x轴交于点A和点B(2,0),与y轴交于点C,其对称轴与x轴交于点D.
如图,二次函数y=ax2+bx+3的图象抛物线与其对称轴交于点(-1,m),与x轴交于点A和点B(2,0),与y轴交于点C,其对称轴与x轴交于点D. 如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.
如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P.