题目内容
6.求下列各式有意义的取值范围:(1)$\frac{2-x}{x}$
(2)$\frac{x}{|x|-1}$
(3)$\frac{x-1}{2x-1}$
(4)$\frac{3}{{x}^{2}-4}$
(5)$\frac{x-1}{\sqrt{x-3}}$
(6)$\frac{2x}{|x-2|+1}$
(7)$\frac{x+2}{{x}^{2}+4}$
(8)$\frac{\sqrt{2x-1}-1}{\sqrt{x+3}}$.
分析 (1)根据分式有意义的条件:分母不为零可得x≠0;
(2)根据分式有意义的条件:分母不为零可得:|x|-1≠0,再解即可;
(3)根据分式有意义的条件:分母不为零可得2x-1≠0,再解即可;
(4)根据分式有意义的条件:分母不为零可得x2-4≠0,再解即可;
(5)根据分式有意义的条件:分母不为零和二次根式有意义的条件可得x-3>0,再解即可;
(6)根据分式有意义的条件:分母不为零可得|x-2|+1≠0,再解即可;
(7)根据分式有意义的条件:分母不为零可得x2+4≠0,再解即可;
(8)根据分式有意义的条件:分母不为零,二次根式有意义的条件可得$\left\{\begin{array}{l}{x+3>0}\\{2x-1≥0}\end{array}\right.$,再解不等式组即可.
解答 解:(1)由题意得:x≠0;
(2)由题意得:|x|-1≠0,
解得:x≠±1;
(3)由题意得2x-1≠0,
解得:x≠$\frac{1}{2}$;
(4)由题意得:x2-4≠0,
解得:x≠±2;
(5)由题意得:x-3>0,
解得:x>3;
(6)由题意得:|x-2|+1≠0,
解得:x为任意实数;
(7)由题意得:x2+4≠0,
解得:x为任意实数;
(8)由题意得$\left\{\begin{array}{l}{x+3>0}\\{2x-1≥0}\end{array}\right.$,
解得:x$≥\frac{1}{2}$.
点评 此题主要考查了分式和二次根式有意义的条件,关键是掌握分式有意义,分母不为0;二次根式的被开方数是非负数.

练习册系列答案
相关题目
19.方程(x-a)(x+b)=0的两根是( )
| A. | x1=a,x2=b | B. | x1=a,x2=-b | C. | x1=-a,x2=b | D. | x1=-a,x2=-b |
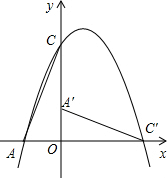 如图,在直角坐标系中,O是坐标原点,点C的坐标是(0,3),抛物线y=-x2+2x+c经过点C,交x轴负半轴于点A.
如图,在直角坐标系中,O是坐标原点,点C的坐标是(0,3),抛物线y=-x2+2x+c经过点C,交x轴负半轴于点A.