��Ŀ����
1��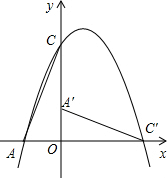 ��ͼ����ֱ������ϵ�У�O������ԭ�㣬��C�������ǣ�0��3����������y=-x2+2x+c������C����x�Ḻ�����ڵ�A��
��ͼ����ֱ������ϵ�У�O������ԭ�㣬��C�������ǣ�0��3����������y=-x2+2x+c������C����x�Ḻ�����ڵ�A����1����c��ֵ����д�������߽���ʽ��
��2������AOC�Ƶ�O˳ʱ����ת90�㣬�õ���A��OC�䣮
�����C������꣬��ͨ�������жϵ�C���Ƿ����������ϣ�
����������������ƽ��m����λ��ʹƽ�ƺ�õ��������߶������ڡ�A��OC����ڲ�����������A��OC��ı߽磩����m��ȡֵ��Χ��ֱ��д���𰸼��ɣ���
���� ��1��ֱ�ӽ�C��������������߽���ʽ�����ó��𰸣�
��2��������������ת�����ʵó�C�����꣬�������������ϵ���������ʵó��𰸣�
�����ȵó������߶������꣬�����ô���ϵ�������ֱ��A��C��Ľ���ʽ����������ֱ���ϵ���������ʵó�m��ȡֵ��Χ��
��� �⣺��1����C��0��3������y=-x2+2x+c��
��ã�c=3��
�������߽���ʽΪ��y=-x2+2x+3��
��2���١�OC=3����OC��=3��
��C��������3��0����
��x=3ʱ��y=-x2+2x+3=0��
���C�����������ϣ�
����ͼ����y=-x2+2x+3
=-��x2-2x��+3
=-��x-1��2+4��
�������ߵĶ�������Ϊ����1��4����
��C������Ϊ��3��0�����Գ���Ϊֱ��x=1��
��A����������-1��0����
��A�����������0��1����
��ֱ��A��C��Ľ���ʽΪ��y=kx+b��
��$\left\{\begin{array}{l}{b=1}\\{3k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=1}\end{array}\right.$��
��ֱ��A��C��Ľ���ʽΪ��y=-$\frac{1}{3}$x+1��
�߽�����������ƽ��m����λ��ʹƽ�ƺ�õ��������߶������ڡ�A��OC����ڲ�����������A��OC��ı߽磩��
�൱x=1ʱ��������ƽ�Ƶ�E�㣬y=-$\frac{1}{3}$x+1=$\frac{2}{3}$����m=4-$\frac{2}{3}$=3$\frac{1}{3}$��
��m��ȡֵ��ΧΪ��3$\frac{1}{3}$��m��4��
���� ������Ҫ�����˺���ͼ���ϵ�����������Լ�����ϵ����һ�κ�������ʽ�Լ��䷽������κ������������ƽ�Ƶ����ʵ�֪ʶ�����ֱ��A��C��Ľ���ʽ�ǽ���ؼ���

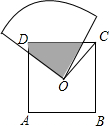 ��ͼ��O�DZ߳�Ϊa��������ABCD�����ģ���һ��뾶�㹻����Բ��Ϊֱ�ǵ�����ֽ���Բ�ķ���O�㴦������ֽ���Բ����O��ת����������ABCD��ֽ�帲�Dz��ֵ����Ϊ��������
��ͼ��O�DZ߳�Ϊa��������ABCD�����ģ���һ��뾶�㹻����Բ��Ϊֱ�ǵ�����ֽ���Բ�ķ���O�㴦������ֽ���Բ����O��ת����������ABCD��ֽ�帲�Dz��ֵ����Ϊ��������| A�� | $\frac{1}{3}$a2 | B�� | $\frac{1}{4}$a2 | C�� | $\frac{1}{2}$a2 | D�� | $\frac{1}{4}$a |
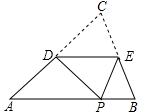 ��ͼ��D��E�ֱ�Ϊ��ABC��AC��BC�ߵ��е㣬������������DE�۵�������CDE=48�㣬���ADP���ڣ�������
��ͼ��D��E�ֱ�Ϊ��ABC��AC��BC�ߵ��е㣬������������DE�۵�������CDE=48�㣬���ADP���ڣ�������| A�� | 42�� | B�� | 48�� | C�� | 84�� | D�� | 58�� |
 ��ͼ��AB��BC��DC��BC��E��BC�ϣ�AB=EC��BE=CD��EF��AD��F����֤��F��AD�е㣮
��ͼ��AB��BC��DC��BC��E��BC�ϣ�AB=EC��BE=CD��EF��AD��F����֤��F��AD�е㣮