题目内容
 如图,?ABCD中,点E是BC的中点.
如图,?ABCD中,点E是BC的中点.(1)若
| AF |
| EF |
| CD |
| CG |
(2)若
| AF |
| EF |
| CD |
| CG |
考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:(1)利用平行四边形的性质得出NE
GC,NE∥AB,AB=CD,进而求出答案;
(2)利用平行四边形的性质得出
=m,进而得出答案.
| ∥ |
. |
| 1 |
| 2 |
(2)利用平行四边形的性质得出
| AB |
| NE |
解答: 解:(1)过点E作EN∥CG于点N,
解:(1)过点E作EN∥CG于点N,
∵?ABCD中,点E是BC的中点,
∴NE
GC,NE∥AB,AB=CD,
∵
=3,
∴
=3,
∴
=
;
(2)∵?ABCD中,点E是BC的中点,
∴NE
GC,NE∥AB,AB=CD,
∵
=m,
∴
=m,
∴
=
.
 解:(1)过点E作EN∥CG于点N,
解:(1)过点E作EN∥CG于点N,∵?ABCD中,点E是BC的中点,
∴NE
| ∥ |
. |
| 1 |
| 2 |
∵
| AF |
| EF |
∴
| AB |
| NE |
∴
| CD |
| CG |
| 3 |
| 2 |
(2)∵?ABCD中,点E是BC的中点,
∴NE
| ∥ |
. |
| 1 |
| 2 |
∵
| AF |
| EF |
∴
| AB |
| NE |
∴
| CD |
| CG |
| m |
| 2 |
点评:此题主要考查了平行四边形的性质,得出
的比值是解题关键.
| AB |
| NE |

练习册系列答案
相关题目
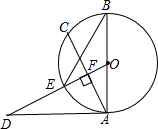 如图所示,⊙O直径AB=10,AD是⊙O的切线,OD⊥弦AC于点F,且交⊙O于点E,有下列结论:
如图所示,⊙O直径AB=10,AD是⊙O的切线,OD⊥弦AC于点F,且交⊙O于点E,有下列结论: