题目内容
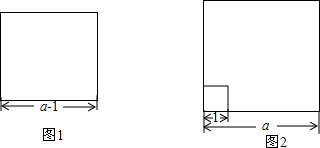
5.有甲、乙两块玉米试验田,甲试验田是边长为(a-1)米的正方形土地(a>1),如图1,玉米的总产量为90千克.乙试验田也是一块正方形的土地,边长为a米,但在其一角有一边长为1米的正方形蓄水池,如图2,乙的玉米总产量为110千克.(1)若甲、乙两块试验田的单位面积产量相等,求a的值;
(2)若甲、乙两块试验田的单位面积产量不相等,那么那块试验田单位面积产量高,为什么?
分析 (1)单位面积产量=总产量÷面积;
(2)根据题意表示出甲乙两农科所的单位产量,比较即可得到结果.
解答 解:(1)依题意得:$\frac{90}{(a-1)^{2}}$=$\frac{110}{{a}^{2}-1}$,
整理,得(a-1)(a-10)=0,
解得a1=1,a2=10;
经检验a1=1不合题意,舍去.
答:若甲、乙两块试验田的单位面积产量相等,求a的值是10;
(2)甲的单位面积产量为$\frac{90}{(a-1)^{2}}$,乙的面积产量为$\frac{110}{{a}^{2}-1}$,
所以$\frac{90}{(a-1)^{2}}$-$\frac{110}{{a}^{2}-1}$=-$\frac{20(a-1)(a-10)}{(a+1)^{2}({a}^{2}-1)}$.
因为a>1,
所以a-1>0,a2-1>0,(a-1)2>0.
当a=10时,甲的单位面积产量=乙的面积产量;
当a>10时,-$\frac{20(a-1)(a-10)}{(a+1)^{2}({a}^{2}-1)}$<0,即$\frac{90}{(a-1)^{2}}$<$\frac{110}{{a}^{2}-1}$,此时,甲的单位面积产量<乙的面积产量;
当a<10时,-$\frac{20(a-1)(a-10)}{(a+1)^{2}({a}^{2}-1)}$>0,即$\frac{90}{(a-1)^{2}}$>$\frac{110}{{a}^{2}-1}$,此时,甲的单位面积产量>乙的面积产量.
点评 本题考查了分式方程的应用.解答(2)题时,要对a的不同取值进行分类讨论,以防错解.

练习册系列答案
相关题目
15. 如图,在等边△ABC中,BC=2,⊙A与BC相切于点D,且与AB,AC分别交于点E,F,则$\widehat{EF}$的长是( )
如图,在等边△ABC中,BC=2,⊙A与BC相切于点D,且与AB,AC分别交于点E,F,则$\widehat{EF}$的长是( )
 如图,在等边△ABC中,BC=2,⊙A与BC相切于点D,且与AB,AC分别交于点E,F,则$\widehat{EF}$的长是( )
如图,在等边△ABC中,BC=2,⊙A与BC相切于点D,且与AB,AC分别交于点E,F,则$\widehat{EF}$的长是( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{\sqrt{3}π}{3}$ | D. | $\sqrt{3}$π |
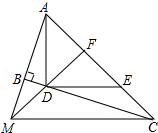 如图,∠ABC=90°,MF⊥AC于F,交BC于D,交AB的延长线于M,连接CM,AF=DF.
如图,∠ABC=90°,MF⊥AC于F,交BC于D,交AB的延长线于M,连接CM,AF=DF.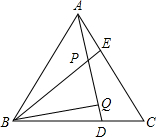 如图,△ABC为等边三角形,AE=CD,AD交BE于点P,BQ⊥AD于Q.
如图,△ABC为等边三角形,AE=CD,AD交BE于点P,BQ⊥AD于Q. 如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.
如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.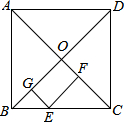 在正方形ABCD中,E为BC边上一点,EF⊥AC,垂足为F,EG⊥BD,垂足为G,BD=6,则EF+EG为3.
在正方形ABCD中,E为BC边上一点,EF⊥AC,垂足为F,EG⊥BD,垂足为G,BD=6,则EF+EG为3.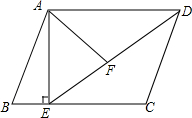 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6$\sqrt{3}$,AF=4$\sqrt{3}$,则AE的长为6.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6$\sqrt{3}$,AF=4$\sqrt{3}$,则AE的长为6.