题目内容
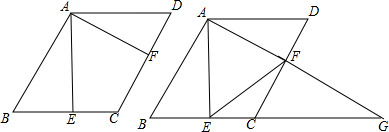
13. 如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.
如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.(1)求证:AP⊥DE;
(2)当∠BAO=15°,求BP的长;
(3)在(2)的条件下,连接DE分别与边AB、AC交于点G、H,判定以DG、GH、HE这三条线段为边构成的三角形是什么特殊三角形,请说明理由.
分析 (1)由△ADP与△AEP是等边三角形,于是得到AD=AE=AP,PD=PE=AP,根据线段垂直平分线的判定定理即可得到结论.
(2)连接PG,若∠DAB=15°,由∠DAP=60°可以得出∠PAG=45°.由已知条件可以得出四边形ADPE是菱形,就有DO垂直平分AP,得到GP=AG,就有∠PAG=∠APG=45°,得出∠PGA=90°,设BG=t,在Rt△BPG中∠APG=60°,就可以求出BP=2t,PG=$\sqrt{3}$t,从而求得t的值,即可以求出结论;
(3)以DG、GH、HE这三条线段为边构成的三角形为直角三角形,由已知条件可知四边形ADPE为菱形,可以得到∠ADO=∠AEH=30°,根据∠DAB=15°,可以求出∠AGO=45°,∠HAO=15°,∠EAH=45°.设AO=a,则AD=AE=2a,OD=$\sqrt{3}$a,得到DG=($\sqrt{3}$-1)a,由∠DAB=15°,可以求出∠DHA=∠DAH=75°,求得GH=(3-$\sqrt{3}$)a,HE=2($\sqrt{3}$-1)a,最后由勾股定理的逆定理就可以得出结论.
解答 (1)证明:∵△ADP与△AEP是等边三角形,
∴AD=AE=AP,PD=PE=AP,
∴AP垂直平分DE,
∴AP⊥DE;
(2)解:如图2,连接PG,
∵∠DAB=15°,
∵∠DAP=60°,
∴∠PAG=45°.
∵△APD和△APE是等边三角形,
∴四边形ADPE是菱形,
∴DO垂直平分AP,
∴GP=AG,
∴∠PAG=∠APG=45°,
∴∠PGA=90°.
设BG=t,在Rt△BPG中,∠ABP=60°,
∴BP=2t,PG=$\sqrt{3}$t,
∴AG=PG=$\sqrt{3}$t,
∴$\sqrt{3}$t+t=2,
解得t=$\sqrt{3}$-1,
∴BP=2t=2$\sqrt{3}$-2;
(3)以DG、GH、HE这三条线段为边构成的三角形为直角三角形.
解:设DE交AP于点O,
∵△APD和△APE是等边三角形,
∴AD=DP=AP=PE=EA,
∴四边形ADPE为菱形,
∴AO⊥DE,∠ADO=∠AEH=30°.
∵∠DAB=15°,
∴∠GAO=45°,
∴∠AGO=45°,∠HAO=15°,
∴∠EAH=45°.
设AO=a,则AD=AE=2a,GO=AO=a,OD=$\sqrt{3}$a.
∴DG=DO-GO=($\sqrt{3}$-1)a.
∵∠DAB=15°,∠BAC=60°,∠ADO=30°,
∴∠DHA=∠DAH=75°.
∴DH=AD=2a,
∴GH=DH-DG=2a-($\sqrt{3}$-1)a=(3-$\sqrt{3}$)a.
HE=DE-DH=2DO-DH=2$\sqrt{3}$a-2a.
∵DG2+GH2=[($\sqrt{3}$-1)a]2+[(3-$\sqrt{3}$)a]2=(16-8$\sqrt{3}$)a2,
HE2=(2$\sqrt{3}$-2a)2=(16-8$\sqrt{3}$)a2.
∴DG2+GH2=HE2,
∴以DG、GH、HE这三条线段为边构成的三角形为直角三角形.
点评 本题考查了等边三角形的性质,菱形的性质和判定,线段垂直平分线的判定,勾股定理的运用.本题的综合性较强,在解答时要注意解答问题的突破口,这也是解答问题的关键.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | 50m | B. | 60m | C. | 70m | D. | 80m |
| A. | (0,0) | B. | (1,-1) | C. | (1,1) | D. | (-1,1) |
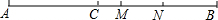 如图,点C是线段AB上一点,M、N分别是AB、CB的中点,AC=8cm,NB=5cm,求线段MN的长.
如图,点C是线段AB上一点,M、N分别是AB、CB的中点,AC=8cm,NB=5cm,求线段MN的长.
 如图,在四边形ABDC中,AD=4,CD=3$\sqrt{2}$,∠ABC=∠ACB=∠ADC=45°,则BD的长是$\sqrt{2}$.
如图,在四边形ABDC中,AD=4,CD=3$\sqrt{2}$,∠ABC=∠ACB=∠ADC=45°,则BD的长是$\sqrt{2}$. 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在边CD上,连接DE,连接BG并延长交CD于点M,交DE于点H,则HM的长为$\frac{3\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在边CD上,连接DE,连接BG并延长交CD于点M,交DE于点H,则HM的长为$\frac{3\sqrt{5}}{5}$.