题目内容
14.若关于x的二次方程(m+1)x2+5x+m2-3m=4的常数项为0,则m的值为4.分析 根据方程常数项为0,求出m的值即可.
解答 解:方程整理得:(m+1)x2+5x+m2-3m-4=0,
由常数项为0,得到m2-3m-4=0,即(m-4)(m+1)=0,
解得:m=4或m=-1,
当m=-1时,方程为5x=0,不合题意,舍去,
则m的值为4.
故答案为:4
点评 此题考查了一元二次方程的一般形式,以及一元二次方程的定义,将方程化为一般形式是解本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
6.下列方程中,是一元一次方程的是( )
| A. | x+3=8+y | B. | x2+5x-3=0 | C. | x+$\frac{1}{x}$=2 | D. | 3x+4=0 |
3.下下列各点中,在函数y=2x-3图象上的点是( )
| A. | (0,0) | B. | (1,-1) | C. | (1,1) | D. | (-1,1) |
4.如果单项式-$\frac{1}{2}$xa+2y3与yb-1x是同项式,那么a,b的值分别为( )
| A. | a=-2,b=4 | B. | a=-1,b=2 | C. | a=-1,b=4 | D. | a=-2,b=2 |
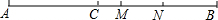 如图,点C是线段AB上一点,M、N分别是AB、CB的中点,AC=8cm,NB=5cm,求线段MN的长.
如图,点C是线段AB上一点,M、N分别是AB、CB的中点,AC=8cm,NB=5cm,求线段MN的长.
 如图,OP是∠MON内的一条射线,点A,B都在OP上,AC⊥OM,AD⊥ON,BE⊥OM、BF⊥ON,垂足分别为C,D,E,F,且AC=AD,求证:BE=BF.
如图,OP是∠MON内的一条射线,点A,B都在OP上,AC⊥OM,AD⊥ON,BE⊥OM、BF⊥ON,垂足分别为C,D,E,F,且AC=AD,求证:BE=BF.