题目内容
20.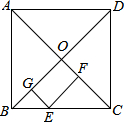 在正方形ABCD中,E为BC边上一点,EF⊥AC,垂足为F,EG⊥BD,垂足为G,BD=6,则EF+EG为3.
在正方形ABCD中,E为BC边上一点,EF⊥AC,垂足为F,EG⊥BD,垂足为G,BD=6,则EF+EG为3.
分析 由正方形ABCD,以及对角线BD的长,得到对角线互相垂直,OB等于BD的一半,根据三个角为直角的四边形为矩形得到四边形GEFO为矩形,进而得到矩形的对边相等,同时得到三角形GEB为等腰直角三角形,由等量代换得到EF+EG=OB,求出即可.
解答 解:∵正方形ABCD,BD=3,
∴∠OBC=45°,BD⊥AC,OB=$\frac{1}{2}$BD=3,
∵EF⊥AC,EG⊥OB,
∴∠OFE=∠OGE=∠BOC=90°,
∴四边形GEFO为矩形,△GEB为等腰直角三角形,
∴OG=EF,BG=EG,
∴EF+EG=OG+GB=OB=3.
故答案为:3.
点评 此题考查了正方形的性质,矩形的判定,以及等腰直角三角形的判定与性质,熟练掌握正方形的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.现有背面完全相同的四张扑克牌,牌面数字分别是2,3,4,5,洗匀后背面朝上,则从中任意翻开一张是2的倍数的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
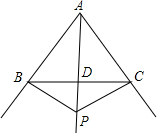 如图,P是∠BAC的平分线上一点,PB⊥AB于B,PC⊥AC于C,BC交PA于点D,下列结论:
如图,P是∠BAC的平分线上一点,PB⊥AB于B,PC⊥AC于C,BC交PA于点D,下列结论: 如图,在四边形ABDC中,AD=4,CD=3$\sqrt{2}$,∠ABC=∠ACB=∠ADC=45°,则BD的长是$\sqrt{2}$.
如图,在四边形ABDC中,AD=4,CD=3$\sqrt{2}$,∠ABC=∠ACB=∠ADC=45°,则BD的长是$\sqrt{2}$.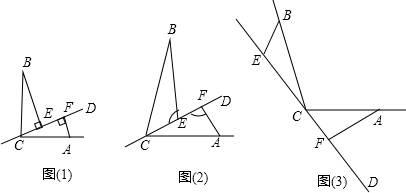
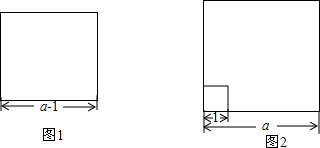
 如图所示,二次函数y1=a(x-b)2的图象与直线y2=kx+b交于A(0,-1)、B(1,0)两点.
如图所示,二次函数y1=a(x-b)2的图象与直线y2=kx+b交于A(0,-1)、B(1,0)两点.