题目内容
7.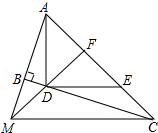 如图,∠ABC=90°,MF⊥AC于F,交BC于D,交AB的延长线于M,连接CM,AF=DF.
如图,∠ABC=90°,MF⊥AC于F,交BC于D,交AB的延长线于M,连接CM,AF=DF.(1)求证:∠FMC=∠FCM;
(2)过D作DE∥CM,交AC于E,求证:AD⊥DE.
分析 (1)证出∠AMF=∠DCF,由AAS证明△AMF≌△DCF,得出对应边相等MF=CF,由等腰三角形的性质即可得出结论;
(2)由等腰三角形的性质和思考虚拟机定理求出∠FCM=45°,由平行线的性质得出∠FED=∠FCM=45°,求出∠FDE=∠FED,得出EF=DF=AF,由线段垂直平分线的性质得出AD=ED,得出∠DAE=∠FED=45°,由三角形内角和定理求出∠ADE=90°,即可得出结论.
解答 (1)证明:∵MF⊥AC,
∴∠AFM=∠DFC=90°,
∴∠AMF+∠BAC=90°,
∵∠ABC=90°,
∴∠DCF+∠BAC=90°,
∴∠AMF=∠DCF,
在△AMF和△DCF中,$\left\{\begin{array}{l}{∠AFM=∠DFC}&{\;}\\{∠AMF=∠DCF}&{\;}\\{AF=DF}&{\;}\end{array}\right.$,
∴△AMF≌△DCF(AAS),
∴MF=CF,
∴∠FMC=∠FCM;
(2)证明:∵∠DFC=90°,MF=CF,
∴∠FCM=45°,
∵DE∥CM,
∴∠FED=∠FCM=45°,
∴∠FDE=90°-45°=∠FED,
∴EF=DF=AF,
∴AD=ED,
∴∠DAE=∠FED=45°,
∴∠ADE=90°,
∴AD⊥DE.
点评 该题主要考查了直角三角形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、平行线的性质、线段垂直平分线的性质等知识;证明三角形全等是解决问题的突破口.

练习册系列答案
相关题目
17.在军事演习中,利用雷达跟踪某一“敌方”目标,需要确定该目标的( )
| A. | 方向 | B. | 距离 | C. | 大小 | D. | 方向与距离 |
15.甲队修路120m与乙队修路100m所用的天数相同,已知甲队比乙队每天多修10m,则甲队每天修路( )
| A. | 50m | B. | 60m | C. | 70m | D. | 80m |
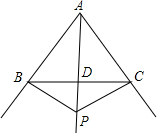 如图,P是∠BAC的平分线上一点,PB⊥AB于B,PC⊥AC于C,BC交PA于点D,下列结论:
如图,P是∠BAC的平分线上一点,PB⊥AB于B,PC⊥AC于C,BC交PA于点D,下列结论: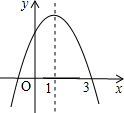 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,下列结论:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,下列结论: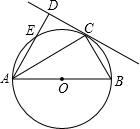 如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线与AD垂直于点D,AD交⊙O于点E,∠B=60°,⊙O的半径为4cm,求CD的长.
如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线与AD垂直于点D,AD交⊙O于点E,∠B=60°,⊙O的半径为4cm,求CD的长.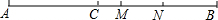 如图,点C是线段AB上一点,M、N分别是AB、CB的中点,AC=8cm,NB=5cm,求线段MN的长.
如图,点C是线段AB上一点,M、N分别是AB、CB的中点,AC=8cm,NB=5cm,求线段MN的长.