题目内容
17.随着私家车的增多,节假日期间,高速公路收费站经常拥堵严重,去年元旦早上8点,某收费站出城方向有120辆汽车排队等候收费通过,假设每分钟到达收费站的汽车数量保持不变,每个收费窗口每分钟可以通过的汽车数量也不变,若开放5个收费窗口,则需要20分钟才能将原来排队等候的汽车及后来到达的汽车全部收费通过;若开放全部6个窗口,只需15分钟.(1)请求出每分钟到达收费站的车辆数以及每个收费窗口每分钟可以通过的车辆数;
(2)为了缓减拥堵,今年元旦节前,该收费站将出城方向的6个窗口中的若干个改造成了ETC通道,已知ETC通道每分钟可以通过10辆车,今年元旦早上8点有130辆车排队等候收费通过,在每分钟到达的汽车数量比去年同期增长50%的情况下,不到5分钟所有排队等候的汽车及后来到达的汽车全部收费通过,请问至少有几个收费窗口改造成了ETC通道?
分析 (1)设每分钟到达收费站的车辆数为x辆,每个收费窗口每分钟可以通过的车辆数为y辆,由题意得等量关系:①5个收费窗口20分钟通过的车的数量=120辆+20分钟到达的车的数量;②6个收费窗口15分钟通过的车的数量=120辆+15分钟到达的车的数量,根据等量关系列出方程组,再解即可;
(2)设有a个收费窗口改造成了ETC通道,由题意得不等关系:[每分钟a个ETC通道通过的车的数量+(6-a)个人工窗口通过的车的数量]×5≥130辆+5分钟到达的车的数量,根据不等关系列出不等式,再解即可.
解答 解:(1)设每分钟到达收费站的车辆数为x辆,每个收费窗口每分钟可以通过的车辆数为y辆,由题意得:
$\left\{\begin{array}{l}{5y×20=120+20x}\\{6y×15=120+15x}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$.
答:每分钟到达收费站的车辆数为4辆,每个收费窗口每分钟可以通过的车辆数为2辆;
(2)设有a个收费窗口改造成了ETC通道,由题意得:
5×[10a+2(6-a)]≥130+(1+50%)×4×5,
解得:a≥2.5,
∵a为整数,
∴a=3.
答:至少有3个收费窗口改造成了ETC通道.
点评 此题主要考查了二元一次方程组和一元一次不等式的应用,关键是正确理解题意,找出题目中的等量关系或不等关系,列出方程组和不等式.

练习册系列答案
相关题目
6.下列方程中,是一元一次方程的是( )
| A. | x+3=8+y | B. | x2+5x-3=0 | C. | x+$\frac{1}{x}$=2 | D. | 3x+4=0 |
7.小明经过市场调查,发现某种鼠标在第x天的售价和相关信息如下表:已知鼠标每件进价50元,设销售该商品的每天的利润为w元.
(1)求w与x的函数关系式;
(2)销售鼠标第几天时,当天的鼠标销售利润最大?最大销售利润为多少?
(3)小明在销售这种鼠标的过程中,共有26天的日销售利润不低于1350元.
| 时间x(天) | 1≤x≤30 |
| 售价(元/件) | x+60 |
| 当天销售(件) | 100-2x |
(2)销售鼠标第几天时,当天的鼠标销售利润最大?最大销售利润为多少?
(3)小明在销售这种鼠标的过程中,共有26天的日销售利润不低于1350元.
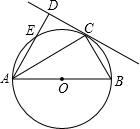 如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线与AD垂直于点D,AD交⊙O于点E,∠B=60°,⊙O的半径为4cm,求CD的长.
如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线与AD垂直于点D,AD交⊙O于点E,∠B=60°,⊙O的半径为4cm,求CD的长. 如图,在四边形ABDC中,AD=4,CD=3$\sqrt{2}$,∠ABC=∠ACB=∠ADC=45°,则BD的长是$\sqrt{2}$.
如图,在四边形ABDC中,AD=4,CD=3$\sqrt{2}$,∠ABC=∠ACB=∠ADC=45°,则BD的长是$\sqrt{2}$.
 如图所示,二次函数y1=a(x-b)2的图象与直线y2=kx+b交于A(0,-1)、B(1,0)两点.
如图所示,二次函数y1=a(x-b)2的图象与直线y2=kx+b交于A(0,-1)、B(1,0)两点.